倒立摆，Inverted Pendulum ，是典型地多变量、高阶次 ，非线性、强耦合、自然不稳定系统。倒立摆系统地稳定控制是控制理论中地典型问题 ，在倒立摆地控制过程中能有效反映控制理论中地许多关键问题 ，如非线性问题、鲁棒性问题、随动问题、镇定、跟踪问题等。因此倒立摆系统作为控制理论教学与科研中典型地物理模型 ，常被用来检验新地控制理论和算法地正确性及其在实际应用中地有效性。

一、原理介绍：

开环系统，状态变量的倒数 = 系统的状态空间矩阵A * 系统状态变量x

A状态矩阵：描述系统本身物理特性的一个矩阵，它是由系统本身的机械结构、物理结构决定的，无法改变。

系统状态变量x：用四个变量描述了倒立摆整个系统的运动状态（倒立摆角度、角速度、飞轮速度、飞轮角速度）。

闭环系统：

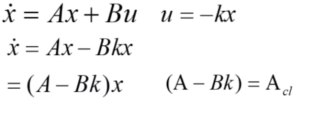
B状态矩阵也是由系统本身的物理特性决定的。u就是反馈项，u = - kx。

整个闭环算法中最重要的就是求出最佳的K，来使得系统稳定。

如何求最优K是核心问题，LQR实际上提供了求解最优K的方法。

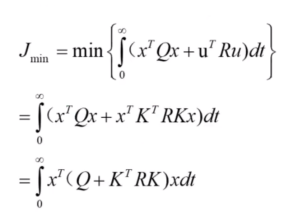
通过代价函数来求K，可以看到里面还有Q和R，这两个与系统的收敛有关。Q是系统状态变量的权重，也叫权重矩阵。

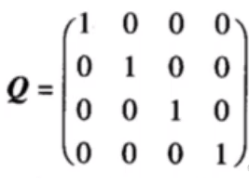
根据这个来看，比如Q11就是倒立摆角度的权重，Q22就是角速度的权重，Q33就是飞轮角度的权重、Q44就是飞轮角速度的权重。如果希望道理摆角度收敛的更快（更快稳定），可以给Q11的权重增加.

R的话，可以理解为决定系统输出量大小的项。一般而言R都设为1,不去改变它。

结合这两个式子

R越大，u的输出越小；R越小，u的输出越大。

一句话，要想求出K，就需要A矩阵、B矩阵、Q矩阵、R矩阵（一般为1）

其实只需要三个。A矩阵和B矩阵得通过建模得到。

物理建模 --- 建立动力学模型（为了A矩阵和B矩阵）

这个是动量轮动力摆系统，可以用牛顿第二定律来分析力，但是我们用更常用的求法。

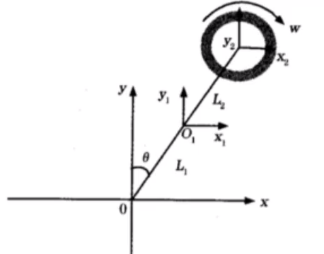
用拉格朗日方程：

因为拉格朗日方程不需要列出系统具体的力是怎样平衡的

它只需要列出系统的动能减去势能得到算子，然后争对这个算子对系统不同的广义坐标求偏导，最后得到系统的广义力

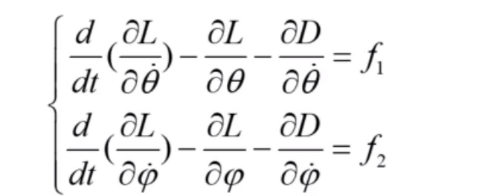
这个θ是摆杆的摆角

这个φ是动量轮自身的转动角度

得：

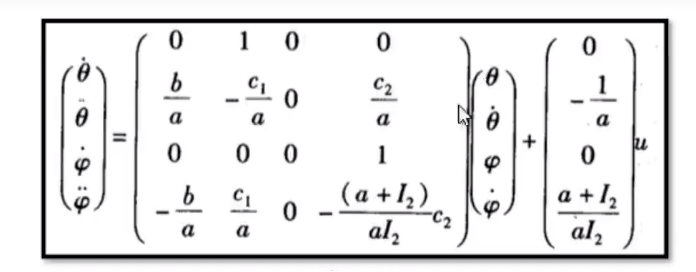
其MATLAB实现为：

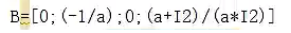
二、实例：

这里介绍“DengFOC动量轮倒立摆项目”

DengFOC动量轮倒立摆是基于SimpleFOC官方开源的动量轮倒立摆项目，低成本化和小型化后应用在开源的DengFOC双路无刷电机驱动器上的DengFOC配套项目。

只要你手头有一块DengFOC V3就可以快速搭接出此项目，项目供电默认电压为16.8V，除DengFOC外，其它电子元器件主要由一个2204无刷电机，两个as5600编码器组成。

其实现代码为：

#include <SimpleFOC.h>

// 无刷直流电机初始化

BLDCMotor motor = BLDCMotor(7); //2208电机

// 定义无刷直流驱动器

BLDCDriver3PWM driver = BLDCDriver3PWM(32,33,25,12);

// 电机编码器初始化

MagneticSensorI2C sensor0 = MagneticSensorI2C(AS5600_I2C);

MagneticSensorI2C pendulum = MagneticSensorI2C(AS5600_I2C);

TwoWire I2Cone = TwoWire(0);

TwoWire I2Ctwo = TwoWire(1);

float adjust_ang= 60;

float adjust_p_vel= 3;

float adjust_motor_vel= 0.18;

float adjust_total_ang= 0; //微调角度

// 通讯命令预设

Commander command = Commander(Serial);

void doTarget_motor_vel(char* cmd) { Serial.print("Change LQR motor_v");command.scalar(&adjust_motor_vel, cmd); }

void doTarget_p_vel(char* cmd) { Serial.print("Change LQR P_v");command.scalar(&adjust_p_vel, cmd); }

void doTarget_ang_vel(char* cmd) { Serial.print("Change LQR ang");command.scalar(&adjust_ang, cmd); }

void doTarget_total_ang(char* cmd) { Serial.print("Change total ang");command.scalar(&adjust_total_ang, cmd); }

void setup() {

// 初始化电机编码器硬件

I2Cone.begin(19,18, 400000UL);

I2Ctwo.begin(23,5, 400000UL);

sensor0.init(&I2Cone);

pendulum.init(&I2Ctwo);

// 设置要使用的控制回路类型

motor.controller = MotionControlType::torque;

// 将电机连接到编码器

motor.linkSensor(&sensor0);

// driver

driver.voltage_power_supply =16.8;

driver.voltage_limit = 16;

driver.init();

// 把电机连接到驱动器上

motor.linkDriver(&driver);

Serial.begin(115200);

motor.useMonitoring(Serial);

// 初始化运动

motor.init();

// 校准编码器并启动FOC

motor.initFOC();

command.add('M', doTarget_motor_vel, "adjust_motor_vel");

command.add('P', doTarget_p_vel, "adjust_p_vel");

command.add('A', doTarget_ang_vel, "adjust_ang");

command.add('T',doTarget_total_ang, "adjust_total_ang");

}

// 循环下采样计数器

long loop_count = 0;

float target_voltage;

void loop() {

// ~1ms

motor.loopFOC();

command.run();

// 控制回路每次~25ms

if(loop_count++ > 25){

// 倒立摆传感器读取

pendulum.update();

sensor0.update();

// 计算摆角

float pendulum_angle = constrainAngle(pendulum.getAngle()-2.6-adjust_total_ang + M_PI);//先看上电串口打印的角度然后替换这里的2.6

Serial.println(pendulum.getAngle());

//Serial.println(sensor0.getAngle());

if( abs(pendulum_angle) < 0.5){ // 如果角度足够小稳定

target_voltage = controllerLQR(pendulum_angle, pendulum.getVelocity(), motor.shaftVelocity());}

else{ // 倒立摆

//Serial.println("swing-up");

// 设置100%的最大电压到电机，以便摆动

//target_voltage = -_sign(pendulum.getVelocity())*motor.voltage_limit*1;

target_voltage = -_sign(pendulum.getVelocity())*16.8;

//Serial.println(target_voltage);

//target_voltage=0;

}

// 将目标电压设置到电机上

motor.move(target_voltage);

// 重置计数器

loop_count=0;

}

}

// 函数限制-和之间的夹角，以-180度和180度表示

float constrainAngle(float x){

x = fmod(x + M_PI, _2PI);

if (x < 0)

x += _2PI;

return x - M_PI;

}

// LQR稳定控制器功能

// 计算需要设置电机的电压，以稳定摆

float controllerLQR(float p_angle, float p_vel, float m_vel){

// 如果角度可控

// 计算控制律

// LQR controller u = k*x

// - k = [40, 7, 0.3]

// - x = [摆角，摆速度，电机速度]'

float u = adjust_ang*p_angle + adjust_p_vel*p_vel + adjust_motor_vel*m_vel;

// 限制设定给电机的电压

//if(abs(u) > motor.voltage_limit*1) u = _sign(u)*motor.voltage_limit*1;

if(abs(u) > driver.voltage_power_supply*0.7) u = _sign(u)*driver.voltage_power_supply*0.7;

return u;

}

来源: 来自于网络