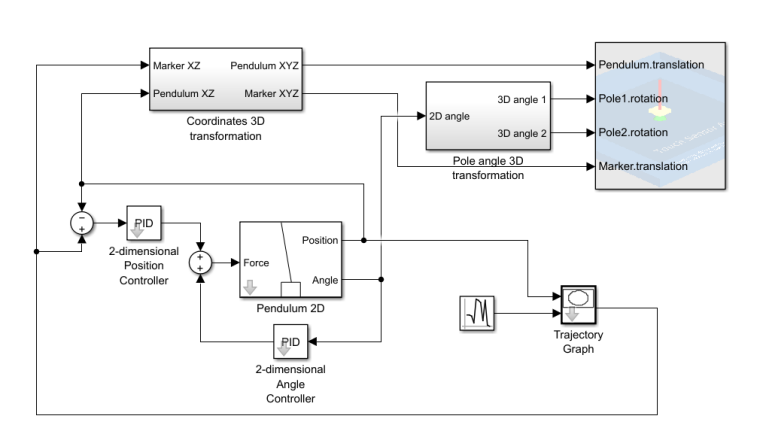
倒立摆最初研究开始于20世纪50年代,麻省理工学院(MIT)的控制论专家根据火警发射助推器原理设计出一级倒立摆实验设备,而后人们又参照双足机器人控制问题研制二级倒立摆控制设备,从而提高了检验控制理论或方法的能力，也拓宽了控制理论或方法的检验范围。三级、四级倒立摆是由一、二级倒立摆演绎而来，其实物系统控制的实现是公认的难题。

2002年8月,著名模糊理论专家李洪兴教授领导的复杂系统智能控制实验室,采用变论域自适应模糊控制在国际上首次度功实现了直线(二维)四级倒立摆的实物系统控制:2010年1月，李洪兴教授领导的科研团队又成功实现了空间四级倒工摆的实物系统控制。

通俗地讲,二级倒立摆是在一个平面上运动的倒立面,n空间倒立摆则是实现了左、右、前、后以及任何方向运动的到立摆，空间四级倒立摆的实物系统控制。

（1）对安装有fuzzy control toolbox，在示例中找到倒立摆，可以在如下画面进行仿真。

（2）虽然摆杆的偏向角0(单位:rad)保持在(一0.05,0.15)内,摆杆向左偏移没有超过3°,向右偏移没有超过9°,但还是不够理想.对于精度要求要求比较高的单输人单输出控制系统，可采用下述方法设计模糊控制器:

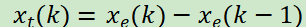
1°根据实际经验或试验得到输出控制量与输入变量偏差的一组数据,并由计算输入变量偏差变化率,将输入变量偏差及偏差变化率从小到大排列(表6.3).这就是说，将输人变量偏差划分为n个等级，输入变量偏差变化率划分为m个等级.

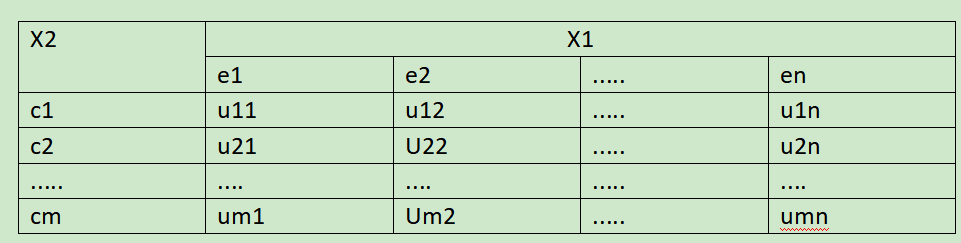
2°建立输入变量偏差及偏差变化率各等级的隶属函数dij(xe,xc)。隶属函数应当满足:当(xe,xc)∈[ej;,ej+1]X[ci,ci+1]时,除了dij,di,j+1,di+1,j,, di+1,j+1外,其他各等级的隶属度都为零,特别当(xi,xe)=(ej,ci)时,dij=1,其他各等级的隶属度都为零.

3°模糊判别方法:对于实际输入变量偏差xe及偏差变化率xc，计算各等级的

隶属度dij。，然后应用公式

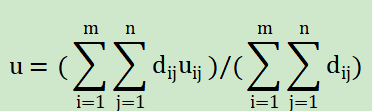
将u作为控制变量的实际输出值.

当控制系统有特别好的线性性时,更直接地采用简化公式，如下面例子所示。

例倒摆的模糊控制器的设计(二)

由于倒摆的控制系统有特别好的线性性,可直接采用下列公式

u=20.75xe+0.25xc。

倒摆的 MATLAB计算机仿真程序如下:

A=[1,1,0,0;20.601,1,0,0;0,0,1,1;-0.4905,0,0,1];

B=[0,-1,0,0.5]';%仿真矩阵

x(1,1)=0.3;x(2,1)=0;x(3,1)=0;x(4,1)=0;%赋初值

for(k=1:200) %进行 200次仿真实验

xe=x(1,k);xc=0;%计算输入变量偏差

if(k>1)xc=x(1,k)-x(1,k-1);

end %计算输入变量偏差的变化率

u(k)=20.75*xe+0.25*xc;%计算实际输出量

x(:,k+1)=A*x(:,k)+B*u(k); %由倒摆运动方程进行仿真

end

t=1:201; y=x(1,:); plot(t,y); %

来源: 成信大，部分来自书籍