5月20日，浙江省沈括科普基金会正式成立。你也许对沈括并不陌生，但真的了解他取得的科学成就吗？听说过他提出的“隙积术”吗？本期科小二为您解读沈括的重要科学成就之一：隙积术！

想象一下，你是一家古代酒坊的掌柜，店里堆满了十几层酒坛，从底层到顶层，每一层的长和宽都比下一层少摆一个坛子。如果让你清点总数，难道要一层层数到天黑吗？别急，北宋“科学全才”沈括早就发明了一个神奇的方法——隙积术，不仅能快速算清酒坛，还意外推动了中国古代数学的飞跃！

连续与离散：酒坛堆中的数学漏洞我们把刚才的数酒坛问题细化一下：假设有这样一堆叠在一起的酒坛，每一层的长和宽都比下一层少摆一个坛子，顶层有2²个，第二层有3²个……底层有12²个，共11层，酒坛总数就是2²+3²+…+12²。

这其实是一个二阶等差数列求和问题。我们平时说的“等差数列”（比如1，3，5，7……）是“一阶等差数列”，相邻两项之间的差是相等的。而像1、4、9、16、25……这样的数列，相邻两项之间的差构成一个等差数列（在这个例子中是3、5、7、9……），这就是“二阶等差数列”。

当时，对于各种实心几何体，大多已经有了现成的体积公式。而酒坛堆垛与棱台接近，能不能用计算棱台体积的“刍童术”来计算酒坛总数呢？

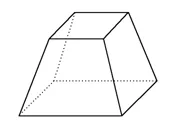
棱台

沈括发现，用刍童术计算酒坛、棋子这类堆叠物的数量时，结果总是比实际数量少。其实，刍童术计算的是实心无缝隙物体的体积，而酒坛堆叠时每层都会空出缝隙，因此套用传统公式会有偏差。

于是他脑洞大开： 既然旧公式不准，那就给它打个“数学补丁”。

几何与级数：堆叠缝隙开启数学新方向沈括将离散问题转化为连续几何模型（如棱台体积），并引入修正项，最终得出了隙积术。

《梦溪笔谈》书影，图源：识典古籍

沈括在《梦溪笔谈》中写道：“余思而得之，用‘刍童法’为上行、下行，别列下广，以上广减之，余者以高乘之，六而一，并入上行。” 这句话用现代语言讲就是：

1. 先按实心体积算：把这种堆垛想象成一个实心的长方棱台，用刍童术算出体积。

2. 再补上缝隙的误差：额外计算一个修正值（即下底宽减上底宽，乘高，除以六），与第一步得到的结果相加。

总结成公式就是：

总数量 = 刍童术结果 + 修正项

修正项 = 层数×(底层宽−顶层宽)/6

沈括用这个公式计算前文提到的11层酒坛，结果是649个，和逐层硬算的结果分毫不差！沈括的公式不仅跳过了逐层计算的麻烦，还精确修正了误差。

古代与现代：隙积术的历史意义隙积术看似只是一个数堆垛物体数目的技巧，却在数学史上投下了一块巨石：

1. 突破传统数学边界：传统几何体积算法仅适用于连续的几何体（无缝隙），而隙积术首次解决了离散堆积物（如酒坛、棋子）的数量计算问题。而且，此前的中国古代数学仅掌握等差级数计算（如1+2+3+…+n），隙积术首次研究二阶等差级数（1²+2²+3²+…+n²），打开了高阶等差级数研究的大门。

2. 启发宋元“垛积术” ：南宋杨辉在《详解九章算法》中发展出三角垛、方垛等公式，元代朱世杰的《四元玉鉴》进一步将垛积术推至四阶、五阶等差级数。

《四元玉鉴细草》书影，图源：百度百科

3. 连续与离散的辩证方法：沈括以连续几何模型解决离散问题，再以修正项弥补间隙误差，体现了“化离散为连续，再回归离散”的辩证思维。此外，隙积术用几何公式解决数列求和问题，体现了中国古代数学的“象数结合”思想（即数形结合）。隙积术既有理论上的突破，又兼顾实用性，成为中国古代数学“经世致用”与逻辑推演结合的典范。

英国科学史家李约瑟高度评价隙积术，认为它是“中世纪中国数学最杰出的成就之一”。当代数学家吴文俊也指出，宋元垛积术中隐含的递推思想，可视为有限差分法的早期雏形。

沈括的隙积术不仅是一项数学成果，更是中国古代科学创新精神的表现。它开创了中国高阶等差级数研究的先河，推动了宋元数学的发展，并在方法论上为后世提供了“连续与离散结合”“实用与理论并重”的宝贵范式。

更令人惊叹的是，沈括这位“跨界大神”还研究过石油开采、磁偏角、节气历法……他用隙积术告诉我们：生活中的难题，往往是科学革命的起点。当你下次面对堆积的物品时，不妨想想沈括——或许下一个改变世界的数学发现，就藏在眼前的缝隙里。

审核专家：邸继征，美国北达科他州立大学高级访问学者、浙江省老教授协会副会长、浙江工业大学教授、应用数学学科负责人、省级精品课程《高等数学》负责人

靠谱出品

撰稿：陈林孝 秘塔AI

来源: 科小二