图文详情

真空中的光速是一个重要的物理学基本常数，通常表示为c，光速的数值是 c=299792458m/s。光的本质是电磁波，光速的数值可以从麦克斯韦方程中推出来。在电磁介质中，光速与介质的介电常数和磁导率有关。

根据相对论，光速是空间中信息和能量传播速度的上限，在不同的惯性参考系中光速不变。狭义相对论还提出了著名的质能方程E=mc²，说明了质量与能量的等价性。

光速在天文学和航空航天中有重要的应用。在地球与航天器的通信中，光速决定了通信信号的延迟。在天文学中，许多天文单位的定义与光速相关。

研究历史

真空中的光速是一个物理常量，国际公认值为c=299792458m/s。17世纪前人们以为光速为无限大，意大利物理学家G.伽利略曾对此提出怀疑，并试图通过实验来检验他设想，在距离很远的两个地方，两人互相用灯光传递信号，最终没能成功。

艾萨克·牛顿也接受光速是有限的观念，在他1704年出版的书《光学》中，他提出光每秒钟可以横越地球16.6次（相当于210，000公里/秒，比正确值低了30%）。这似乎是他自己的推断（不能确知他是否有引用或参考罗默的数据）。

1676年，丹麦天文学家奥劳斯·罗默（1644~1710）利用木星卫星的星蚀时间变化证实光是以有限速度传播的。他利用木星的木卫一在木星在木星圆面上的投影作周期性变化的现象，第一次定量的估计出光速。艾欧的公转轨道可以用来计算时间，因为它会规律的进入木星的阴影中一段时间。罗默观测到当地球在最接近木星时，艾欧的公转周期是42.5小时，当地球远离木星时，艾欧从阴影中出现的时间会比预测的越来越晚，很明显的是因为木星与地球的距离增加，使得"信号"要花更多的时间传递。光要通过行星之间增加的距离，使得计时的信号在第一次和下一次之间因而延长了额外的时间。当地球向木星接近时，情形则正好相反。罗默观测到艾欧在接近的40个轨道周期中周期比远离的40个轨道周期缩短了22分钟。以这些观测为基础，罗默认为在80个轨道周期中光线要多花费22分钟行走艾欧与地球之间增加的距离。这意味着地球经历了80个艾欧轨道周期（42.5小时）的时间，光线只要花22分钟。这对应于一个地球在轨道上绕着太阳运动和光速之间的一个比例。意味着光速是地球的轨道速度的9，300倍，与现在的数值10，100倍比较，相差较小。但是因为这种观测是很困难的，因而日后被其他的方法所取代。

在当时，天文单位的估计数值是大约1.4亿公里。克里斯蒂安·惠更斯结合了天文单位和罗默的时间估计，每分钟的光速是地球直径的1，000倍，他似乎误解了罗默22分钟的意思，以为是横越地球轨道所花费的时间。这相当于每秒22万公里（13.6万英里），比现在采用的数值低了26%，但仍比当时使用其他已知的物理方法测得的数值为佳。

即使如此，靠着这些观测，光速是有限的，仍不能被大众满意接受（著名的有吉恩·多米尼克·卡西尼），直到在詹姆斯·布雷德里（1728）的观测之后，光速是无限的想法才被放弃。布雷德里推论若光速是有限的，则因为地球的轨道速度，会使抵达地球的星光有一个微小角度的偏折，这就是所谓的光行差，他的大小只有1/200度。布雷德里计算的光速为298，000公里/秒（185，000英里/秒），这与现在的数值只有不到1%的差异。光行差的效应在19世纪已经被充分的研究，最著名的学者是瓦西里·雅可夫列维奇·斯特鲁维。

1849年，法国物理学家A.H.L.菲佐用旋转齿轮法首次在地面实验室中成功地进行了光速测量，最早的结果为c=315000千米/秒。1862年，法国实验物理学家J.-B.-L.傅科根据D.F.J.阿拉戈的设想用旋转镜法测得光速为c=（298000±500）千米/秒。19世纪中叶J.C.麦克斯韦建立了电磁场理论，他根据电磁波动方程曾指出，电磁波在真空中的传播速度等于静电单位电量与电磁单位电量的比值，只要在实验上分别用这两种单位测量同一电量（或电流），就可算出电磁波的波速。1856年，R.科尔劳施和W.韦伯完成了有关测量，麦克斯韦根据他们的数据计算出电磁波在真空中的波速值为3.1074×10^5千米/秒，此值与菲佐的结果十分接近，这对人们确认光是电磁波起过很大作用。

1926年，美国物理学家A.A.迈克耳孙改进了傅科的实验，测得c=（299796±4）千米/秒，他于1929年在真空中重做了此实验，测得c=299774千米/秒。后来有人用光开关（克尔盒）代替齿轮转动以改进菲佐的实验，其精度比旋转镜法提高了两个数量级。1952年，英国实验物理学家K.D.费罗姆用微波干涉仪法测量光速得c=（299792.50±0.10）千米/秒。此值于1957年被推荐为国际推荐值使用，直至1973年。

1972年，美国的K.M.埃文森等人直接测量激光频率ν和真空中的波长λ，按公式 $v%3D%5Ctext%7B%20%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Cmu_0%5Cvarepsilon_0%7D%7D$ （其中v为真空中电磁波的速度，为真空磁导率，为真空介电常数）算得c=（299792458±1.2）米/秒。1975年第15届国际计量大会确认上述光速值作为国际推荐值使用。1983年17届国际计量大会通过了米的新定义，在这定义中光速c=299792458米/秒为规定值，而长度单位米由这个规定值定义。既然真空中的光速已成为定义值，以后就不需对光速进行任何测量了。

1983年，光速取代了保存在巴黎国际计量局的由90%铂和10%铱的合金制成的米原器被选作定义“米”的标准，并且约定光速严格等于299，792，458m/s，此数值与当时的米的定义和秒的定义一致。后来，随着实验精度的不断提高，光速的数值有所改变，米被定义为 $%5Cfrac%7B1%7D%7B299%2C792%2C458%7D$ 秒内真空中光通过的路程。

1849年，菲索用旋转齿轮法求得。他是第一位用实验方法，测定地面光速的实验者。实验方法大致如下：光从半镀银面反射后，经高速旋转的齿轮投向反射镜，再沿原路返回。如果齿轮转过一齿所需的时间，正好与光往返的时间相等，就可透过半镀银面观测到光，从而根据齿轮的转速计算出光速。

1862年，法国的傅科用旋转镜法测空气中的光速，原理和斐索的旋转齿轮法大同小异，他的结果是。

第三位在地面上测到光速的是考尔纽。1874年他改进了菲索的旋转齿轮法，得。

阿尔伯特·迈克耳孙改进了傅科的旋转镜法，多次测量光速。1879年，得；1882年得。后来，他综合旋转镜法和旋转齿轮法的特点，发展了旋转棱镜法，1924～1927年间，得。

迈克耳逊在推算真空中的光速时，应该用空气的群速折射率，可是他用的却是空气的相速折射率。这一错误在1929年被经改正后，1926年的结果应为。

后来，由于电子学的发展，用克尔盒、谐振腔、光电测距仪等方法，光速的测定，比直接用光学方法又提高了一个数量级。

60年代雷射器发明，运用稳频雷射器，可以大大降低光速测量的不确定度。

1973年达0.004 ppm，终于在1983年第十七届国际计量大会上作出决定，将真空中的光速定为精确值。

早期认识

公元前五世纪的古希腊哲学家恩培多克勒（Ἐμπεδοκλῆς）是第一个提出光的理论的人，他认为光的速度是有限的3。而亚里士多德（Ἀριστοτέλης Aristotélēs）认为：“光是由于某物的存在但它不是一种运动”4。欧几里得（Εὐκλείδης）和托勒密（Πτολεμαῖος）在恩培多克勒理论的基础上，提出了光的视觉发射理论：光从眼睛中发出，从而使视觉成为可能。基于该理论，亚历山大港的赫仑（Ἥρων）认为光速必须是无限的，因为遥远的物体在睁开眼睛时会立即出现5。

1021年，阿尔哈曾（أبو علي، الحسن بن الحسن بن الهيثم）出版了《光学之书》，反驳了光的视觉发射理论，认为光线是从物体进入眼睛的6。他认为光速是有限的，而且是可变的。在密度较大的物体中光速会减小7。他还认为光是实质的物质，光的传播时需要时间的，但不会被我们感受到8。

早期的测量

1629年，艾萨克·贝克曼（Isaac Beeckman）提出了一项测量光速的实验：让一个人观察大炮从远处的镜子反射回来的闪光。1638年，伽利略·伽利莱（Galileo Galilei）提出了一个实验：通过观察开灯与一定距离外的人对灯光的感知之间的延迟来测量光速。他的结论是：如果光的传播不是瞬时的，那么一定非常迅速以至于这个实验中的人来不及反应9。

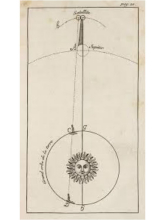1676年，奥勒·克里斯滕森·罗默（Ole Christensen Rømer）首次对光速进行了定量估计10。他观察到地球接近木星时木星最内层卫星木卫一圆轨道运动的周期比地球远离木星时短，据此推测光大概需要22分钟才能走过地球轨道的直径的距离。克里斯蒂安·惠更斯（Christiaan Huygens）根据对地球轨道的直径的估计和奥勒·克里斯滕森·罗默的观测结果，估计光速的数值是，这比实际值低大约。11

1704年，艾萨克·牛顿（Iassc Newton）在报告中汇报了自己根据罗默的数据对光速的估算：太阳光到地球所需时间大约七到八分钟。牛顿听说罗默观测到的日食阴影不是彩色的，他得出结论：不同颜色的光传播速度相同12。

19世纪，阿曼德·伊波利特·路易斯·菲索（Armand Hippolyte Louis Fizeau）设计了一个测量光速的实验：在8633米外放一面镜子，让出射光线和镜子的反射光线通过一个快速旋转的齿轮。当齿轮转的足够快时，反射光会射到齿轮上，实验者看不见反射光。通过这个方法，他测得光速是13。

电磁学理论的发展

856年，威廉·爱德华·韦伯（Wilhelm Eduard Weber）和鲁道夫·科尔劳什（RudolfKohlrausch）通过莱顿瓶放电测得 $%5Cfrac1%7B%5Csqrt%7B%5Cvarepsilon_0%5Cmu_0%7D%7D$ 的数值很接近真空中光速。次年，古斯塔夫·基尔霍夫（Gustav Kirchhoff）计算出无电阻导线中的电信号以这个速度传播14。

19世纪60年代初，詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell）提出了他的电磁理论。根据他的电磁理论，真空中电磁波传播的速度是 $%5Cfrac1%7B%5Csqrt%7B%5Cvarepsilon_0%5Cmu_0%7D%7D$ 。他提出光是一种电磁波15。

以太理论

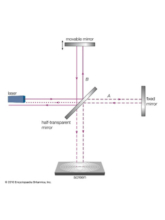19世纪，物理学家认为光在以太介质中传播。当时物理学家提出，可以根据光速的各向同性来测量地球相对于以太介质的运动速度。其中最著名的实验是迈克尔孙-莫雷实验。实验发现：物体相对于以太的运动速度始终为零。16

根据这个实验，亨德里克·洛伦兹（HendrikLorentz）提出装置通过以太的运动可能会导致装置沿其运动方向收缩。据此，他提出了洛伦兹变换的理论，这推动了相对论理论的建立17。

精确测量

自20世纪下半叶开始，腔共振、激光干涉仪等技术极大地提高了光速测量的精度，科学界也做了很多测量光速的实验。1975年，第15届世界计量大会建议使用的值作为真空中光速的标准值18。

1983年，第17届国际计量大会将米重新定义为光在真空中运动 $%5Cfrac1%7B299792458%7Ds$ 经过的路径长度19。

近代测量真空中光速实验的简表：

|| ||

（注：esu即electrostatic units的缩写；emu为electromagnetic units的缩写。）

理论推导

真空中的电磁波

光速的数值可以是通过麦克斯韦方程组推导出来的。麦克斯韦方程组是

$%5Cbegin%7Baligned%7D%26%5Cvec%7B%5Cnabla%7D%5Ccdot%20E%3D-%5Cfrac%7B%5Crho%7D%7B%5Cvarepsilon_%7B0%7D%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%3D%5Cmu_%7B0%7D%5Cvec%7BJ%7D%2B%5Cvarepsilon_%7B0%7D%5Cmu_%7B0%7D%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D%5Cend%7Baligned%7D$ （2）

在真空中，没有电荷和电流，麦克斯韦方程组是

$%5Cbegin%7Baligned%7D%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BE%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%3D%5Cvarepsilon_%7B0%7D%5Cmu_%7B0%7D%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D%5Cend%7Baligned%7D$ （3）

前两个方程告诉我们，电磁波必定是横波，电场和磁场都垂直于波的传播方向。对后两个公式求旋度，得到

$%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%5Cright%29%3D%5Cvec%7B%5Cnabla%7D%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BE%7D%5Cright%29-%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%5Cright%29%7D%7B%5Cpartial%20t%7D%5CRightarrow%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BE%7D%3D%5Cvarepsilon_0%5Cmu_0%5Cfrac%7B%5Cpartial%5E2%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%5E2%7D%5C%5C%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%5Cright%29%3D%5Cvec%7B%5Cnabla%7D%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%5Cright%29-%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BB%7D%3D%5Cvarepsilon_0%5Cmu_0%5Cfrac%7B%5Cpartial%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%5Cright%29%7D%7B%5Cpartial%20t%7D%5CRightarrow%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BB%7D%3D%5Cvarepsilon_0%5Cmu_0%5Cfrac%7B%5Cpartial%5E2%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%5E2%7D$ （4）