余弦定理,一般是指在欧氏平面的三角形中关于三边长度和一个角度余弦值的恒等式。借助余弦定理,可以在已知三角形两边及其夹角的情况下,算出第三边的长度;也可以在已知三边长度的情况下,算出各角的余弦值。
余弦定理可以用于解三角形、构造恒等式等。
余弦定理可以推广至四边形、四面体、高维空间、非欧空间等,具有深刻的内涵。
定理内容
在 中的余弦定理为
中的余弦定理为

其中 ,
, ,
, 为
为 的三边长。
的三边长。
上式还可以写为:

发展简史
余弦定理是一条重要的几何定理,其发展贯穿了古代数学的演进,涉及多个文明的贡献。最早关于余弦定理的思想可以追溯到古希腊数学家欧几里得的《几何原本》。尽管他没有明确提出余弦定理,但书中第2卷命题12和13涉及类似的关系,讨论了三角形边长和角之间的代数关系1。
而到了中世纪时期,阿拉伯数学家阿尔-胡瓦里兹米和阿尔-图西对三角学进行了更深入的研究。他们系统地总结了球面三角学和平面三角学中的基本定理。其中阿尔-图西首次在球面三角学中明确提出了余弦定理的球面版本。2
在欧洲文艺复兴时期,数学家们从阿拉伯文献中重新发现了希腊和印度数学,余弦定理得以系统化。德国数学家雷焦蒙塔努斯在15世纪发展了三角学,使余弦定理的推广更为明确。2
17世纪以来,余弦定理被明确用现代的三角函数形式表示简化了数学家的研究和应用,
成为分析三角形问题的基础工具。3现代研究者还进一步扩展了余弦定理,将其应用于非欧几里得几何和高维空间的研究。4
定理证明
余弦定理的证明有许多种方法,这里举如下几例。
利用勾股定理
过点 作
作 边上的高,垂足为点
边上的高,垂足为点 。
。
当 时,点
时,点 在线段
在线段 (含端点)上。
(含端点)上。

故而 ,
, 。令
。令 ,则由勾股定理可知
,则由勾股定理可知


两式相减消去变量 即可得
即可得

当 时,
时, ,由勾股定理立得
,由勾股定理立得
当 时,点
时,点 在线段
在线段 的反向延长线上。
的反向延长线上。
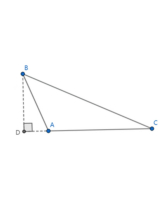
故而 ,
, 。令
。令 ,则由勾股定理可知
,则由勾股定理可知

两式相减消去变量 即可得
即可得

因而 对任意三角形均成立。同理地,
对任意三角形均成立。同理地, 和
和 也成立。定理得证。
也成立。定理得证。
平面向量
在 中满足向量关系
中满足向量关系

等式两侧平方可得

即
同理可证得 和
和 。定理得证。
。定理得证。
利用正弦定理
在 中满足
中满足 ,故而
,故而

由三角形正弦定理5

等比例带入可得

同理可证得 和
和 。定理得证。
。定理得证。
利用面积
以 为边作正方形,则
为边作正方形,则
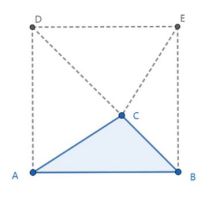

代入面积关系

可知

同理有

任意两式相加后减去第三个式子即得

定理得证。
相关定理
射影定理
在 中的射影定理为
中的射影定理为

射影定理又被称作“第一余弦定理”。借助射影定理可以实现正弦定理和余弦定理的互推。6
勾股定理
当 为直角三角形时,不妨
为直角三角形时,不妨
来源: 百度百科
内容资源由项目单位提供


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助
 百度百科
百度百科 