牛顿运动定律是牛顿力学的基础，描述了力与运动的关系。牛顿运动定律主要包含三个定理：

牛顿第一定律：如果一个物体不受力或所受合外力为0，那么这个物体将保持静止或匀速直线运动。

牛顿第二定律：物体的动量随时间的变化率与受力成正比。

牛顿第三定律：相互作用的两个物体之间的作用力和反作用力大小相等，方向相反，作用在同一条直线上。

这三个定律最早在1687年由艾萨克·牛顿（Isaac Newton）在他的《自然哲学的数学原理》中提出。在这之后，后人在牛顿运动定律的基础上发展了一个完整的力学体系，但牛顿运动定律也有其局限性。一般而言，当物体运动速度非常快或质量非常大时，就需要考虑相对论的修正；而当物体的质量或尺度非常小时，常常需要用到量子力学理论。

定理

牛顿第一运动定律

牛顿第一定律从拉丁文翻译过来，内容如下：

每个物体都会保持静止状态，或做匀速直线运动，除非它被施加在其上的力改变这种运动状态。59

物体有保持原有运动状态的趋势，这被称为惯性。而力是改变物体运动状态的原因。

牛顿第二运动定律

牛顿第二运动定律的原始表述是：

物体的运动变化与受力成正比，并且方向指向力的方向。60

牛顿所说的“运动”指的是动量，它是一个矢量，定义是质量与速度矢量的乘积，即

在实际情况中，质量、力和速度都有可能随时间变化。一般地，牛顿第二运动定律的数学表达式是

如果质量不随时间变化，那么我们常用牛顿第二定律的如下表达式

作用在物体上的力符合矢量叠加的法则，因此物体运动状态改变的方向是合力的方向。对于质点，如果所受合力为零，那么质点的动量就不会改变，此时我们称之为质点处于机械平衡状态。

最初，牛顿第二定律是用加速度来表示的物体运动状态的改变。牛顿第二定律常被认为是定义了力。因此，可以说牛顿第二定律可以说为力与运动的研究提供了一个框架。

牛顿第三运动定律

牛顿第三定律原文的翻译是：

对于每一个行动，总是有一个对立的相等的反应；或者说，两个物体对彼此的互动总是相等的，并且指向对立的方向。61

现在，我们常常将牛顿第三定律表述为：相互作用的两个物体之间的作用力和反作用力大小相等，方向相反，作用在同一条直线上。

与动量守恒的关系

牛顿第三定律与动量守恒定律密切相关。动量守恒定律是物理学中最基本的几个定律之一，即使在量子力学和量子场论中，动量守恒定律依然成立。在牛顿力学中，如果两个物体的动量分别是，那么体系的总动量是。动量守恒定律是说：如果一个体系不受外力或者合外力为0，那么这个体系的动量保持不变。也就是说

根据牛顿第二定律，我们可以看到，作用在两个物体上的力等大反向，这就是牛顿第三定律。

研究历史

公元前5世纪，古希腊哲学家德谟克利特（Leucippus，公元前500-公元前440）、伊壁鸠鲁（Epicurus，公元前341-公元前270）认为：“当原子在虚空里被带向前进而没有东西与他们碰撞时，它们一定以相等的速度运动。”这只是猜测或推想的结果。10

公元前4世纪，古希腊哲学家亚里士多德（Aristotle，公元前384-公元前322）指出：静止是物体的自然状态，如果没有作用力就没有运动（力是维持物体运动的原因）。该观点遗失了“力能使物体停止运动，也能使物体开始运动”这一关键点，故错误。26但他第一次提出了力与运动间存在关系，为力学发展做出了一定贡献。7

6世纪， 希腊学者菲洛彭诺斯（J.Philoponus）对亚里士多德的运动学说持批判态度。他认为抛体本身具有某种动力，推动物体前进，直到耗尽才趋于停止，这种看法后来发展为14世纪的“冲力理论”。10

14世纪，法国哲学家布里丹（Jean Buridan，1295-1358？）、阿尔伯特、尼克尔·奥里斯姆（Nicole Oresme，1320？-1382）等人提出“冲力理论”，他们认为：“推动者在推动一物体运动时，便对它施加某种冲力或某种动力，速度越大，冲力越大，冲力耗尽时，物体停止下来。”这一理论为意大利物理学家伽利略·伽利雷（Galileo Galilei，1564-1642）和英国物理学家艾萨克·牛顿（Isaac Newton，1643-1727）开辟了道路。10

17世纪，伽利略在其的著作中多次提出类似于惯性原理的说法。他分别于1632年和1638年，在《关于托勒密和哥白尼两大世界体系的对话》和《关于力学和位置运动的两门新科学的对话》中记录了理想斜面实验（一小球沿倾斜平台滚向水平面，表面越光滑小球滚得越远27），并推理“如有一足够长而绝对光滑的表面，将没有东西（摩擦力）能阻碍小球运动，所以小球一直继续运动或者直到有东西（外力）阻碍它”，从而得到结论：“物体在自然状态下会维持原有运动而非趋于停止”。该结论打破了自亚里士多德以来约一千三百年间“力是维持物体运动的原因”的陈旧观念，但仍未摆脱其影响。该结论很接近惯性定律（牛顿第一运动定律又称惯性定律，其首先是由伽利略发现的3）。72728

1644年，法国物理学家勒内·笛卡尔（Rene Descartes，1596-1650）在《哲学原理》中弥补了伽利略的不足。29他明确地指出，除非物体受到外因的作用，物体将永远保持其静止或运动状态，并且还特地声明，惯性运动的物体永远不会使自己趋向曲线运动，而只保持在直线上运动。他把这条基本原理表述为两条定律：①每一单独的物质微粒将继续保持同一状态，直到与其他微粒相碰被迫改变这一状态为止；②所有的运动，其本身都是沿直线的。然而笛卡儿没有建立起他试图建立的那种能演绎出各种自然现象的体系，不过他的思想对牛顿对此类定律之后的总结产生了一定的影响。笛卡儿的最大贡献在于他第一个认识到：力是改变物体运动状态的原因。730

1662年，伽利略指出：“以任何速度运动着的物体，只要除去加速或减速的外因，此速度就可以保持不变。”笛卡尔也认为：“在没有外加作用时，粒子或者匀速运动，或者静止。”牛顿把这一假定作为牛顿第一运动定律，并将伽利略的思想进一步推广到有力作用的场合，提出了牛顿第二运动定律。731

1664年，牛顿受到对碰撞问题研究较早的笛卡尔的影响，也开始研究二个球形非弹性刚体的碰撞问题。1665-1666年，牛顿又研究了二个球形刚体的碰撞问题。他没有把注意力集中在动量和动量守恒方面，而是把集中在物体之间的相互作用上。对于两刚体的碰撞，他提出：“在它们向彼此运动的时间中（就是它们相碰的瞬间），它们的压力处于最大值，……它们的整个运动是被此一瞬间彼此之间的压力所阻止，……只要这两个物体都不互相屈服，它们之间将会持有同样猛烈的压力，……它们将会像以前弹回之前彼此趋近那样多的运动相互离开。”32

1668-1669年，荷兰物理学家克里斯蒂安·惠更斯（Christiaan Huygens，1629-1695）、沃里斯（willis）和英国物理学家克里斯托弗·雷恩（Christopher Wren，1632-1723）分别对碰撞问题也做了很多研究，并得出了一些重要的结论。33其中，惠更斯的工作比较突出，他证明了两硬体在碰撞过程中同一方向的动量保持不变，纠正了笛卡尔不考虑动量具有方向性的错误，而且首次提出碰撞前后的动量守恒。牛顿在正式提出牛顿第三运动定律时，肯定了他们的工作，同时也指出了他们的局限性。牛顿认为：“雷恩和惠更斯的理论以绝对硬的物体为前提，而用理想弹性体可以得到更肯定的结果，并且用非理想弹性体，如压紧的木球、钢球和玻璃球做实验，消除误差后结果是一致的。”32

1673年，法国物理学家马里奥特（EdmeMarotte，1620-1684）用两个单摆做碰撞实验，巧妙地测出了碰撞前后的瞬时速度。牛顿也重复做了此实验，他进一步讨论了空气阻力的影响及改进办法，并对结果进行了修正。28

1684年8月起，在英国物理学家埃德蒙多·哈雷（EdmondHalley，1656-1742）的劝说下，牛顿开始写作《自然哲学的数学原理》，系统地整理手稿，重新考虑部分问题。1685年11月，形成了两卷专著。1687年7月5日，《原理》使用拉丁文出版。《原理》的绪论部分中的运动的公理或定律一节中提出了牛顿运动定律，摆脱了旧观念的束缚。1713年，《原理》出第2版；1725年，出第3版。73435363738

19世纪后半期，德国物理学家古斯塔夫·罗伯特·基尔霍夫（Gustav Robert Kirchhoff，1824-1887）、奥地利及捷克物理学家恩斯特·马赫（Ernst Mach，1838-1916）、美国物理学家埃森布德（L. Eisenbud）、美国物理学家奥斯顿（N. Austern）等人对牛顿运动定律的表述均有论述，并提出自己的修正意见。其中，马赫在《发展中的力学》39中，对牛顿运动定律做了比较全面的考察和分析整理；埃森布德在《关于经验的运动定律》40中、奥斯顿在《牛顿力学的表述》41中，也提出了相似的新表述。42但这些修正意见中有一部分受到质疑，质疑者包括瑞士及美国物理学家阿尔伯特·爱因斯坦（Albert Einstein，1879-1955）等。43

1905年以来，爱因斯坦的相对论推翻了牛顿建立的大部分科学体系。爱因斯坦指出，牛顿运动定律在超出经典力学范围或质点、惯性参考系以及宏观、低速运动问题等适用条件时，不再成立。该部分内容已超出对牛顿运动定律发展简史的讨论范围，后续发展可参阅狭义相对论、广义相对论等词条。4344

实验验证

牛顿运动定律主要的理论推导或实验验证方法

方法概述

图示

牛顿第一运动定律

伽利略的理想斜面实验：

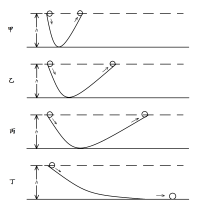
牛顿第一运动定律存在逻辑同一之循环论证9，可通过理想实验对该定律进行理论推导10。

现实中，当球沿斜面向下滚时速度增大，上滚时则减小。由此可知，球沿水平面滚动时，速度应不变。

但事实上由于存在摩擦阻力，球速会越来越慢直至最后停下，且表面越光滑球便会滚得越远。由此可知，若没有摩擦阻力，球将永远滚下去。

若球沿一个光滑斜面从静止状态开始下滚，小球将滚上另一个斜面达到与原来的高度然后再下滚；减小斜面倾角后，小球在另一个斜面上仍达到同一高度但滚得远些。由此可知，斜面平放时，球将永远滚下去。

此即，力不是维持物体的运动（速度）的原因。一旦物体具有某一速度且不受外力，就将保持这一速度匀速直线地运动下去。1112

牛顿第二运动定律

用打点计时器验证：

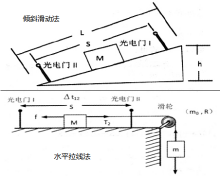
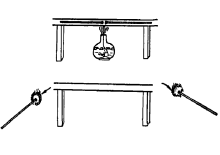
研究系统的加速度与系统的质量和拉力间的关系时，将打点计时器固定在木板的一端，把砝码和小车栓在细线的两端，细线跨过滑轮，砝码的重量作为拉力，让拖着纸带的小车在平直的平面上运动，则小车及其上的砝码、线的另一端栓着的钩码组成一个运动系统。

每次实验均须在纸带上注明拉力和系统的质量。

为了抵消摩擦力，通常采取如右图所示的两种方法：倾斜滑动法、水平拉线法。13

在气垫导轨上验证：

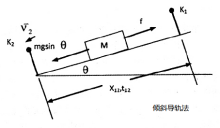
将气垫导轨调平后（由于导轨都存在一定的弯曲，滑块与导轨间存在阻力，所以调平在实验中一般用滑块通过两个光电门时的速度相等来衡量），测出粘性阻尼常数b。

为了修正粘滞性摩擦阻力的存在所引起的速度损失，必须解决对粘滞性阻尼常数的测定。

为了消除粘滞性阻尼，通常采取以下两种方法：倾斜导轨法（如右图所示）、振动法。13

用非线性回归法验证：

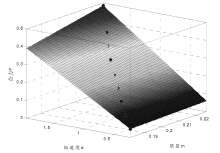
即使是在气垫导轨上验证牛顿第二运动定律，也会有空气阻力作为主要影响因素影响实验测量精度。这需要尝试通过修正，其将影响减小到可忽略的程度。但常采用的一元线性回归法，不足以说明整个回归方程的好坏；二元线性回归法也同样存在一定的问题。14

用非线性回归法验证定律，首先对质点运动的动力学模型进行线性化处理，得到模型的参数线性估计值，并以其作为非线性模型的初值对动力学模型进行非线性回归分析。15

非线性回归法验证了定律的正确性，改进了验证定律的传统实验方法，具有一定的应用和推广价值。15

此外，验证牛顿第二运动定律还有基于LabVIEW的教学平台16、基于无线模块和Visual Basic的仿真演示实验设计17、基于光电传感器的实验装置18等。

牛顿第三运动定律

运用传感器进行定量实验：

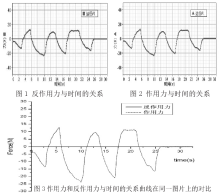
使用两个力传感器并保持两个传感器在同一平面上，让两个传感器的测力钩相互钩住或相抵。通过数据采集软件，分别得到两条力-时间图线，如右图1和图 2所示；同时得到该时间段的作用力和反作用力随时间变化的实时数据。

通过观察可以看出作用力和反作用力与时间的对应关系：任意时刻，这两个力的大小基本一致。这表示这两个力的大小相等。

这种实验方案，不仅适用于量化水平面上的相互作用力，而且适用于量化竖直平面或与竖直方向成任意角度的同一平面上的相互作用力，只要和两个力处于同一平面，就可以精确模拟作用力与反作用力，体现了两个物体之间的作用力和反作用力总是大小相等，作用在同一直线上，更加直观有效地突出牛顿第三运动定律的普适性。19

运用观察法进行定性实验：

取一根长约15厘米两端开口的细玻璃管，管的直径约3毫米（能使火柴进出）。

用两根火柴装入管中，使火柴头在管的中间互相接触，然后放平。用酒精灯对准火柴头加热、不久因玻璃管受热升温。火柴头达到着火点迅速燃烧，气体相互压迫，两根火柴杆从两管的开口处同时飞出，并观察到继续燃烧。

由两火柴头飞出的路程大致相等，可说明物体间的作用力是相互的。此即直观地验证了牛顿第三运动定律。20

（牛顿运动定律的验证性实验有多种，本节仅挑选几种重要或典型的实验作为示例。随着现代的实验设施的利用，原来的实验方法将有所改进或补充。212223）

应用

理论上，根据牛顿运动定律，可以求解所有非相对论经典力学的动力学问题。只要知道了力的表达式，我们就可以计算出运动所满足的方程。

自由落体运动

如果一个物体在地球表面附近以静止的状态坠落，在忽略空气阻力的情况下，物体将以加速度保持不变的直线运动落下，这就是自由落体运动。根据万有引力公式，地心引力大小是：

其中是万有引力常数；分别，是地球和下落物体的质量；是离地心的距离。在离地球不远处，可以认为是地球半径。因此重力加速度是

如果物体并非从静止开始下落，而是有一个平行于地面的速度，那么物体的运动可以被分解为水平方向的匀速运动和竖直方向的匀加速直线运动，物体的运动轨迹将会是抛物线。

曲线运动

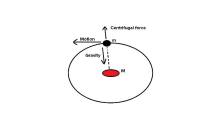先考虑最简单的匀速圆周运动的情况。匀速圆周运动并不是匀速运动，因为速度的方向时刻在变化，有一个加速度。设角速度是，那么圆周运动的速度是。其中的大小是物体单位时间转过的角度，方向可以用右手定则来确定：用手握住旋转的方向，大拇指的方向即的方向。因此，匀速圆周运动的角速度和维持匀速圆周运动需要的力是

来源: 百度百科

内容资源由项目单位提供