对数的概念在历史上对数学和科学的发展起到了重要的推动作用。随着计算需求的增加，尤其是在航海、天文学和工程等领域，数学家们需要一种有效的方法来简化复杂的乘法和除法运算。对数应运而生，并被广泛应用于多个学科。

对数的历史背景

对数的历史可以追溯到17世纪，约翰·纳皮尔（John Napier）是对数概念的首创者。其在1614年发布了《对数之奇迹》，开创了对数的使用。之后，亨利·布里吉斯（Henry Briggs）在1620年引入了常用对数（底为10）的概念，使其在实际应用中更为方便。

对数的基本概念

对数是一个将乘法转化为加法的运算，使得复杂的数学计算变得简单。对数在现代数学中具有重要的地位，是学习代数和微积分的基础。

对数的定义

数学定义

对数是数学中一个重要的概念，主要用于解决指数方程。设且，，则对数的定义为：

这一定义表明，是使得底数的次方等于的指数。对数可以看作是指数运算的逆运算，提供从结果反推底数和指数的帮助。

对数的符号表示

对数通常用符号表示。例如，表示以为底的的对数。

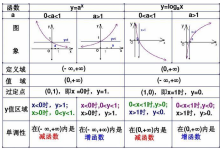
对数的图像与行为

对数函数的图像特征如下：

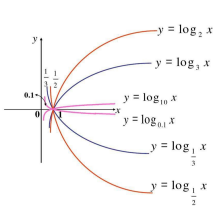
- 当时，，这意味着任何数的零次方都是1。

- 对数函数在时是单调递增的，随着的增大，也会逐渐增大，但增长速度逐渐减缓。

- 当时，，这表明对数函数在接近0时会趋向于负无穷。可以将对数和指数进行比较，可以看到

通过对数的定义和性质，方便了科学、工程、计算机科学等多个领域中有效地进行复杂的计算和分析。

对数的类型

对数根据其底数的不同，可以分为多种类型，每种类型在不同的领域有着广泛的应用。常用的对数有：

常用对数**（十进制对数）**：，通常简写为。在科学和工程中，常用对数非常普遍，特别是在处理大范围数值时，例如分贝（dB）的计算。

自然对数**（底为e的对数）**：，通常写作，其中是自然对数的底数。自然对数在微积分和数学分析中具有重要意义，尤其是在连续增长和衰减的模型中。

二进制对数：，在计算机科学中常用，用于分析算法的复杂度。例如，二分查找算法的时间复杂度为，其中是待搜索的元素数量。1

常用对数（底为10）

常用对数是以10为底的对数，记作或简写为。常用对数在许多工程、科学和商业领域中具有重要应用，特别是在处理涉及数量级差异的情况时。例如：

- 在化学中，pH值的计算使用常用对数，定义为：

其中是氢离子的浓度，pH值的变化反映了溶液酸碱度的变化。

- 在地震学中，里氏震级的计算也使用常用对数，震级可以表示为：

其中是测得的波幅，是基准波幅。震级的对数性质使得可以有效地描述大范围内的地震强度变化。

自然对数（底为 e 的对数）

自然对数是以（约为2.71828）为底的对数，记作。自然对数在微积分和数学分析中具有特殊意义，尤其是在连续增长和衰减模型中。自然对数的主要应用包括：

- 在人口模型中，连续增长的模型常使用自然对数。假设某种生物的数量随时间增长，则可以用下列方程表示：

其中是初始数量，是增长率。对数可以用来线性化这一指数增长模型。

- 在经济学中，自然对数用于计算复利和经济增长模型。例如，复利公式可以表示为：

自然对数在此情况下提供了简洁的表达方式，使得复杂的计算变得更易于处理。

其他对数（如二进制对数）

二进制对数是以2为底的对数，记作。在计算机科学中，二进制对数常用于描述算法的复杂度，帮助分析数据结构和算法效率。其应用示例如下：

- 在信息理论中，香农熵（Shannonentropy）用于量化信息的不确定性，计算公式为：

其中是事件发生的概率。二进制对数在此帮助定义信息量的度量。

- 在算法分析中，许多搜索和排序算法的时间复杂度用二进制对数表示。例如，二分查找算法的复杂度为，这表明随着数据规模的增加，查找时间仅以对数级别增长。

通过以上的分析，我们可以看到，不同类型的对数在各种学科中发挥着重要作用，帮助我们更好地理解和处理现实世界中的问题。

对数的性质

乘法性质

对数的乘法性质是：

这表示对数运算可以将乘法转化为加法，从而简化计算。

除法性质

对数的除法性质为：

这一性质使得对数在处理比例和比率时更加便利。

幂法性质

对数的幂法性质为：

这意味着在计算幂时，可以将对数运算中的指数提到前面。

换底公式

换底公式为：

此公式允许在不同底数之间进行转换，灵活使用。

对数的应用及实例

科学领域（如化学中的pH值）

在化学中，pH值是用来表示溶液酸碱度的指标，定义为氢离子浓度的负对数：

例如，若某溶液中氢离子浓度为，则：

这表示该溶液是酸性的。

来源: 百度百科

内容资源由项目单位提供