牛顿-莱布尼兹公式，又称微积分基本定理，最初指微积分理论中由牛顿和莱布尼兹两人分别独立发现的求定积分的方法。该公式将函数的定积分与原函数联系起来，为计算提供了简便的方法。这不仅是一个用于计算的重要的积分公式，也是分析学的基本公式。

牛顿-莱布尼兹公式可以拓展到高维空间、高阶导数。在现代数学中，随着勒贝格积分理论、测度理论的发展，微积分基本定理的形式也能得到拓展。

1 发展简史

1.1 牛顿：流数与反微分

牛顿把方程看作是一条水平直线和一条垂直直线的交点轨迹，这两条直线运动的速度被称作“流数”，分别为和。1

它们的比恰为对的导数。

有了上述的关系式后，牛顿提出了一个反问题，即“反微分问题”1：给定流数比与之间的关系，试用的表达式求出。用现代的数学语言来阐述，即解微分方程：

牛顿最早于1666年10月借助反微分给出了一个计算面积的方法，被认为是历史上第一次以明显形式出现的微积分基本定理：

其中表示曲线下的面积

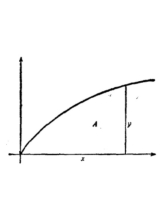
图源：参考资料1图8.3

1.2 莱布尼兹：微分与反切线

在莱布尼兹的微积分体系中，图形面积用一系列高为，宽为的无穷多个小矩形之和来表示，即

为了得到一个图形的面积，莱布尼兹通过它的割圆曲线来求解。

假设一条曲线的纵坐标为，可以求出一条纵坐标为的曲线使得

其中是常数。此时

所以，在莱布尼兹给出的微积分基本定理中，求面积问题转为反切线问题1。令上式中的，则只需找到一条曲线满足

并假设曲线通过坐标原点，则

莱布尼兹在1684年首次发表这些关于微分的结果时并没有进行足够的无穷小量考察，只称这是“一种适用的新方法、一种值得注意的演算”1。

1.3 归属权之争

牛顿在微积分的建立过程当中，对符号表示法并没有表现出兴趣，而是重点关注用这些工具来解决一些特殊的问题；莱布尼兹则一直以一般化的方法和符号体系为工作重点。

牛顿关于微积分的奠基性工作是在1664年到1666年完成的，而莱布尼兹的工作是在1672年到1676年完成的。但是，莱布尼兹在1684年和1686年首先发表了他的结果，牛顿则是首先在他的同事之中散发手稿，直到1687年的《自然科学的数学原理》和1704年的《光学》之后，才正式把他的微积分工作发表出来。

在十七世纪九十年代后期，莱布尼兹开始受到牛顿的继承人的攻击。他们认为莱布尼兹得到和利用了牛顿此前的结果，但并未致谢，公开指责他进行了剽窃。对此，莱布尼兹在1711年向伦敦皇家学会提出申诉，期间，莱布尼兹是会员而牛顿是会长。在次年的判决中，皇家学会任命的委员会认定莱布尼兹有罪。

这场论战是不幸的。与其说是数学上的分歧，不如说是因为英国和欧洲数学家之间的民族主义敌对情绪导致了这些；只要对两人的工作做仔细的研究，就会发现两人的贡献显然是各自独立完成的。1

后来，在这场纷争中取得“胜利”的英国数学家们坚持牛顿的传统方法，排斥莱布尼兹的解析方法，在一段时间内脱离了数学发展的主流。不可否认，牛顿的成就促成了数学和各种其它科学的进步，但这些更多地依赖于莱布尼兹的微积分方法。

2 公式内容

在黎曼积分的意义下，牛顿-莱布尼兹公式的表述如下：

定理（牛顿-莱布尼兹公式 / 微积分基本定理） 如果函数是连续函数在区间上的一个原函数（即：），那么

该公式的右侧有时也写作。

该公式给出了用原函数计算定积分的方法，是一个用于计算的重要的积分公式，也是分析学的一个基本公式。如果将公式拓展至无穷区间，或者在区间边界无界的情形，牛顿-莱布尼兹公式有时也成立，此时的定积分被称为“反常积分”或“瑕积分”。

3 公式证明

给定上的一个连续函数，可以借此在上定义出如下的函数：

该函数被称为积分上限的函数2，并且具有下面的性质：

定理 如果在上连续，那么可导，且。

证明：对于，取使得，那么

于是

若则取，若则取，即可同理得证。

由上述定理，即可证明牛顿-莱布尼兹公式。

证明：由上述定理，是的一个原函数。因而如果也是的一个原函数，则

其中为常数。代入即得

再令即得

移项即得牛顿-莱布尼兹公式在时成立。

如果，只需利用

来源: 百度百科

内容资源由项目单位提供