极值分布是指在概率论中极大值(或者极小值)的概率分布,从很多个彼此独立的值中挑出来的各个极大值应当服从的概率密度分布数f(x)。
定义
设![]() 为从总体F抽出的独立同分布样本,且
为从总体F抽出的独立同分布样本,且
![]() 如果存在常数
如果存在常数![]() 及
及![]() ,使
,使![]() 依分布收敛于G(x),则称G(x)为一极大值分布;类似地定义极小值分布。它们统称为极值分布,而分布F称为“底分布”。
依分布收敛于G(x),则称G(x)为一极大值分布;类似地定义极小值分布。它们统称为极值分布,而分布F称为“底分布”。
两个分布函数![]() 和
和![]() 称为是同类的,若存在常数a>0及b,使
称为是同类的,若存在常数a>0及b,使![]() ,并记为
,并记为![]() 。
。
显然,这种关系具有自反、对称和传递性。
极值分布的三大类型(Fisher—Tippett Theorem):若G(x)为一连续极值分布,则G必与下列三个分布函数之一同类:
![]()
![]()
![]()
![]() 分别称为第Ⅰ、Ⅱ、Ⅲ型极值分布,也分别称为Gumbel、Fr6cht、Weibull型极值分布。
分别称为第Ⅰ、Ⅱ、Ⅲ型极值分布,也分别称为Gumbel、Fr6cht、Weibull型极值分布。
一般的Gumbel型极值分布为
![]() 相应的生存函数为
相应的生存函数为
![]() 当T服从威布尔分布且有密度函数式一般的Gumbel型极值分布时,
当T服从威布尔分布且有密度函数式一般的Gumbel型极值分布时,![]() 就服从
就服从![]() 和众数为
和众数为![]() 的一般Gumbel型极值分布。1
的一般Gumbel型极值分布。1
Gumbel型极值分布
极小值分布
最小极值Ⅰ型分布简称极小值分布,其分布密度函数和分布函数分别为
![]() 及
及
![]()
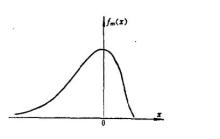 式中
式中 ![]() ——位置参数,实际上是分布的众数;
——位置参数,实际上是分布的众数;![]() ——尺度参数,与分布的离散性有关。
——尺度参数,与分布的离散性有关。
必须注意,![]() 和
和![]() 不是分布的均值及标准差,但与它们有关,分布密度函数式的图形见图1。图1中曲线为
不是分布的均值及标准差,但与它们有关,分布密度函数式的图形见图1。图1中曲线为![]() 的情况,由图1可知,极小值分布为一偏态分布(左偏)。
的情况,由图1可知,极小值分布为一偏态分布(左偏)。
1.标准极小值分布,
令![]() ,则
,则![]() ,代入上述分布密度函数和分布函数式子中得到Z的密度函数及分布函数分别为
,代入上述分布密度函数和分布函数式子中得到Z的密度函数及分布函数分别为
![]()
![]()
上两式称为标准极小值分布,并且与分布参数![]() 及
及![]() 无关。
无关。
2.标准极小值分布的期望值及方差,
![]() 令
令![]() ,代入上式得
,代入上式得
![]() 上式积分为一常数,称作欧拉(Euler)常数。通常记为“
上式积分为一常数,称作欧拉(Euler)常数。通常记为“![]() ”即
”即
![]() 又
又
![]() 所以
所以
![]()
3.极小值分布的期望值及方差,
因为
![]() 所以
所以
![]()
及
![]()
如果已知样本的试验数据,则可以计算总体的均值及标准差的估计值![]() 及s,再由
及s,再由![]() 和
和![]() 的等式可以得到极小值分布的位置参数
的等式可以得到极小值分布的位置参数![]() 及尺度参数
及尺度参数![]() 的估计值:
的估计值:
![]()
极大值分布
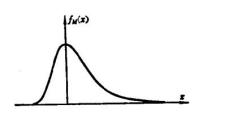
最大极值Ⅰ型渐近分布密度函数和分布函数分别为
![]()
![]()
式中,![]() ——位置参数;
——位置参数;![]() ——尺度参数。
——尺度参数。
极大值分布密度函数的图形如图2所示。
1.标准极大值分布
![]() 令,则
令,则![]() ,代入最大极值Ⅰ型渐近分布密度函数和分布函数两式中,得到
,代入最大极值Ⅰ型渐近分布密度函数和分布函数两式中,得到
![]() 及
及
![]() 上两式称为标准极大值分布密度函数及分布函数,它们与分布参数
上两式称为标准极大值分布密度函数及分布函数,它们与分布参数![]() 无关。
无关。
标准极大值分布的期望值及方差分别为
![]()
![]()
内容资源由项目单位提供


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助
 百度百科
百度百科 