图文详情

电磁波是电磁场随时间变化产生的波，它可以由带电粒子在加速运动的过程中发射变化的电磁场通过电磁波辐射能量和动量，电磁辐射会对发出电磁波的粒子产生辐射反作用。

在真空中，电磁波以光速（通常用C表示）传播（光是电磁波），在介质中电磁波的波速与介质的介电常数和磁导率有关，但不会超过真空中的光速，电磁波频谱由频率或波长来表征。按照频率从小到大排序，电磁波主要包括无线电波、微波、红外线、可见光、紫外线、X射线和伽玛射线。可见光波长范围大概在400-700nm之间。

在量子力学中，电磁波可以看作传递相互作用的光子。

发展历史

19世纪初，人们发现了可见光以外的电磁辐射。1800年，德裔英国天文学家威廉·赫歇尔（William Herschel）发现了红外辐射。赫歇尔用棱镜折射太阳光时发现，对应光谱红色以外的位置温度会升高，他推断太阳光中存在一些不可见的“热射线”，这些热射线后来被称为红外线4。

1801年，德国物理学家约翰·威廉·里特（Johann Wilhelm Ritter）发现了紫外线。他注意到，太阳光谱中紫色一侧光谱之外的位置的不可见射线比紫光更快地使氯化银试剂变暗，他将其称为“化学射线”。后来这种射线被称为紫外线56。里特的实验是摄影术的先驱。

1864年，詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell）提出了电磁场方程组9。通过麦克斯韦方程组可以解出真空中电磁波的方程，并得到电磁波波速是常数“光速”的结论。因此，麦克斯韦推断可见光以及光谱中不可见部分都是电磁波。在1887年，海因里希·赫兹（Heinrich Hertz）首次制造了比可见光频率低得多的电磁波，并开发了检测这些波的方法。这些电磁波被分为无线电波和微波7。

1895年11月8日，威廉·伦琴（Wilhelm Rontgen）在对真空管施加高压时，他注意到附近的一块镀膜玻璃板上出现了荧光。在之后的实验中，他发现这种实验现象是由X射线导致的7。

伽玛射线是在对辐射的研究中发现的。亨利·贝克勒尔（HenriBecquerel）发现，在覆盖纸上的铀盐可以引起未曝光的照相版起雾。玛丽·居里（Marie Curie）发现只有某些特定的元素可以释放能量引起照相版起雾，并且镭可以释放强烈的辐射。1900年，保罗·维拉德（Paul Villard）发现了一种带中性电荷且穿透力极强的辐射，欧内斯特·卢瑟福（Ernest Rutherford）意识到这种辐射一定不是粒子（在那时科学界还没有认识到波粒二象性），并将其命名为伽玛射线。1910年，威廉·亨利·布拉格（William Henry Bragg）证明了伽玛射线不是粒子。1914年，卢瑟福和爱德华·安德拉德（Edward Andrade）测量了伽玛射线的波长，发现其波长比X射线更短7。

基本理论

麦克斯韦方程组

电磁波是根据麦克斯韦方程组推导出来的。麦克斯韦发现了位移电流，描述了变化的电场也会产生磁场，这体现在对安培定理的修正上。麦克斯韦方程是：

$%5Cbegin%7Baligned%7D%26%5Cvec%7B%5Cnabla%7D%5Ccdot%20E%3D-%5Cfrac%7B%5Crho%7D%7B%5Cvarepsilon_%7B0%7D%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%3D%5Cmu_%7B0%7D%5Cvec%7BJ%7D%2B%5Cvarepsilon_%7B0%7D%5Cmu_%7B0%7D%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D%5Cend%7Baligned%7D$ (1)

其中 $%5Cvarepsilon_0%5Cmu_0%5Cfrac%7B%5Cpartial%5Cbar%7BE%7D%7D%7B%5Cpartial%20t%7D$ 是位移电流项。通过麦克斯韦方程组可以推出电磁波的传播速度是一个常数：

$c%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Cvarepsilon_0%5Cmu_0%7D%7D%3D299792458m%5Ccdot%20s%5E%7B-1%7D$ (2)

这个速度被称为光速。在介电常数和磁导率分别是的电磁介质中，光速是 $%5Cfrac1%7B%5Csqrt%7B%5Cvarepsilon%5Cmu%7D%7D$

电磁波方程的推导

在真空中，没有电荷和电流，麦克斯韦方程组是

$%5Cbegin%7Baligned%7D%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BE%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%3D0%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%7D%5C%5C%26%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%3D%5Cvarepsilon_%7B0%7D%5Cmu_%7B0%7D%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D%5Cend%7Baligned%7D$ (3)

前两个方程告诉我们，电磁波必定是横波，电场和磁场都垂直于波的传播方向。对后两个公式求旋度，得到

$%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%5Cright%29%3D%5Cvec%7B%5Cnabla%7D%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BE%7D%5Cright%29-%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%5Cright%29%7D%7B%5Cpartial%20t%7D%5CRightarrow%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BE%7D%3D%5Cvarepsilon_0%5Cmu_0%5C%3A%5Cfrac%7B%5Cpartial%5E2%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%5E2%7D%5C%5C%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%5Cright%29%3D%5Cvec%7B%5Cnabla%7D%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BB%7D%5Cright%29-%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BB%7D%3D%5Cvarepsilon_0%5Cmu_0%5C%3A%5Cfrac%7B%5Cpartial%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%5Cright%29%7D%7B%5Cpartial%20t%7D%5CRightarrow%5Cvec%7B%5Cnabla%7D%5E2%5Cvec%7BB%7D%3D%5Cvarepsilon_0%5Cmu_0%5C%3A%5Cfrac%7B%5Cpartial%5E2%5Cvec%7BB%7D%7D%7B%5Cpartial%20t%5E2%7D$ (4)

其中用到了矢量分析中常用的公式。上述推导得到电磁波随时间变化的方程满足波动方程，相应地波速为 $c%3D%5Cfrac1%7B%5Csqrt%7B%5Cvarepsilon_0%5Cmu_0%7D%7D$ （参见词条“波动方程”）。在介电常数和磁导率分别为的介质中电磁波波速应当修正为 $c%3D%5Cfrac1%7B%5Csqrt%7B%5Cvarepsilon%5Cmu%7D%7D$ 。达朗贝尔算符的定义是

$%5Csquare%3D%5Cfrac%7B1%7D%7Bc%5E%7B2%7D%7D%5Cfrac%7B%5Cpartial%5E%7B2%7D%7D%7B%5Cpartial%20t%5E%7B2%7D%7D-%5Cvec%7B%5Cnabla%7D%5E%7B2%7D$ (5)

因此电磁波方程还可以写成

(6)

根据波动方程的通解，我们可以先得到电磁波方程中电场的解：

(7)

其中是一个常数向量，是任意二阶可微的函数，是传播方向上的波矢。根据第一个麦克斯韦方程，我们可以得到电磁波的一个性质：

(8)

即电场垂直于电磁波传播的方向。根据 $%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BE%7D%3D-%5Cfrac%7B%5Cpartial%20B%7D%7B%5Cpartial%20t%7D$ ，我们可以得到

$%5Cvec%7BB%7D%3D%5Cfrac%7B%5Cvec%7Bk%7D%7D%7Bc%7D%5Ctimes%5Cvec%7BE%7D$ (9)

因此我们可以得到电磁波的一个性质：电场、磁场、电磁波传播方向互相垂直。像研究波动方程一样，研究电磁波时，我们常常取电磁波传播方向为轴，关注其平面波形式

$%5Cvec%7BE%7D%3D%5Cvec%7BE%7D_0e%5E%7Bi%28kz-ct%29%7D%5Cquad%5Cvec%7BB%7D%3D%5Cfrac%7B1%7D%7B%5Cnu%7D%5CBig%28%5Chat%7Bk%7D%5Ctimes%5Cvec%7BE%7D%5CBig%29$ (10)

其中是波速，是电磁波传播方向的波矢.

能量与动量流

考虑一个在电磁场中运动的粒子，我们可以计算电磁场对带电粒子的力做的功：

(11)

一般地，我们可以考虑电流分布。设电荷密度是，电流密度矢量是，那么在体积中，。根据麦克斯韦方程组(3)，可以得到

$%5Cvec%7BE%7D%5Ccdot%5Cvec%7BJ%7D%3D%5Cfrac%7B1%7D%7B%5Cmu_0%7D%5Cvec%7BE%7D%5Ccdot%5Cleft%28%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%5Cright%29-%5Cvarepsilon_0%5Cvec%7BE%7D%5Ccdot%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D$ (12)

根据矢量分析中的公式和麦克斯韦方程组，应用散度定理，进一步计算得到

$%5Cfrac%20d%7Bdt%7D%5CBigg%5BW%2B%5Cint_V%5CBigg%28%5Cfrac12%5Cvarepsilon_0E%5E2%2B%5Cfrac1%7B2%5Cmu_0%7DB%5E2%5CBigg%29dV%5CBigg%5D%3D-%5Cfrac1%7B%5Cmu_0%7D%5Ciiint_S%5CBig%28%5Cvec%7BE%7D%5Ctimes%5Cvec%7BB%7D%5CBig%29%5Ccdot%20d%5Cvec%7BS%7D$ (13)

考虑上式的物理意义，我们可以看到 $%5Cfrac12%5Cvarepsilon_0E%5E2%2B%5Cfrac1%7B2%5Cmu_0%7DB%5E2$ 中两项分别描述电场和磁场的能流密度。 $%5Cfrac1%7B%5Cmu_0%7D%5Ciint_S%5Cleft%28%5Cbar%7BE%7D%5Ctimes%5Cbar%7BB%7D%5Cright%29%5Ccdot%20d%5Cbar%7BS%7D$ 一项表示电磁辐射。单位时间内电磁场通过单位表面积向外传递的能量被称为坡印廷矢量，表达式是

$%5Cvec%7BS%7D%3D%5Cfrac1%7B%5Cmu_0%7D%5CBig%28%5Cvec%7BE%7D%5Ctimes%5Cvec%7BB%7D%5CBig%29$ (14)

反射与折射

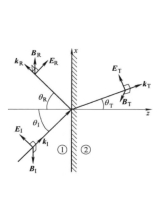
电磁波反射与折射的物理图像如右图所示。我们考虑一束平面波从介质1入射，与这束波有关的物理量下标是，然后在界面处发生反射和折射。与反射有关的物理量下标是，与折射有关的物理量下标是。入射、反射、折射的电磁波均可表示成

$%5Cvec%7BE%7D%3D%5Cvec%7BE%7D_%7B0%7De%5E%7Bi%5Cleft%28%5Cvec%7Bk%7D%5Ccdot%5Cvec%7Br%7D-%5Comega%5Ctau%5Cright%29%7D%5Cquad%5Cvec%7BB%7D%3D%5Cfrac%7B1%7D%7B%5Cnu%7D%5CBig%28%5Chat%7Bk%7D%5Ctimes%5Cvec%7BE%7D%5CBig%29$ (15)