菱形是一种特殊的平行四边形，定义为有一组邻边长度相等的平行四边形。在对几何图形的分析中，菱形的性质有助于解决各种几何问题。

定义

有一组邻边相等的平行四边形是菱形。

如果平行四边形满足，则四边形是菱形。

性质

性质定理：边

菱形的四条边长相等。

证明：设菱形，由定义知四边形是平行四边形，且

由平行四边形的性质1可知

故而可得，该性质得证。

性质定理：对角线

菱形的对角线相互垂直平分，且每条对角线都平分菱形的一组对角。

证明：设菱形，由是平行四边形可知对角线、互相平分1，并设其相交于 。那么点为线段的中点。

由菱形的定义可知，则由等腰三角形的性质2可知。故可得、， 相互垂直平分。

由可知，而由平行四边形对边平行可知。因而，即平分。同理可知平分，平分和。

故而该性质定理得证。

判定

判定定理1

对角线垂直的平行四边形是菱形。

证明：由平行四边形性质可知对角线、互相平分1。而由可知、互相垂直平分，故有。

由菱形定义即知四边形是菱形。该判定定理得证。

判定定理2

四条边相等的四边形是菱形。

证明：由，，可由平行四边形的判定定理3得知四边形是平行四边形。而，则可由菱形的定义得四边形是菱形。该判定定理得证。

判定定理3

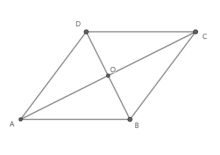对角线垂直且每条对角线都平分一组对角的四边形是菱形。

证明：如图，在和中有

则（判定依据为ASA）。故而。同理可知,则由判定定理2可知四边形ABCD是菱形。该判定定理得证。

应用举例

例1 在矩形中，点在边上，与关于直线对称，点的对称点在边上，过点作，交、于点、。

(1) 连接，求证：四边形

来源: 百度百科

内容资源由项目单位提供