匀变速直线运动，速度均匀变化的直线运动，即加速度不变的直线运动。其速度时间图象是一条倾斜的直线，表示在任意相等的时间内速度的变化量都相同，即速度（v）的变化量与对应时间（t）的变化量之比保持不变（加速度不变），这样的运动是变速运动中最简单的运动形式，叫做匀变速直线运动。1

基本公式

速度-时间公式：

位移**-时间公式**：;6

速度**-位移公式**：;

其中a为加速度，为初速度, 为末速度,t为该过程所用时间，x为该过程中的位移。

位移变化量-时间公式：

代表相邻相等时间段内位移差，T代表相邻相等时间段的时间长度

条件

物体作匀变速直线运动须同时符合下述两条：

（1）所受合外力不为零，且保持不变；

（2）合外力与初速度在同一直线上。

分类

在匀变速直线运动中，如果物体的速度随着时间均匀增加，这个运动叫做匀加速直线运动；如果物体的速度随着时间均匀减小，这个运动叫做匀减速直线运动。

若速度方向与加速度方向相同（即同号），则是加速运动；若速度方向与加速度方向相反（即异号），则是减速运动。

规律推导

一、位移公式推导：

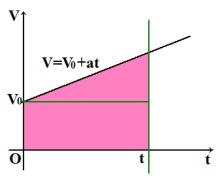
（1）由于匀变速直线运动的速度是均匀变化的，故平均速度=（初速度+末速度）/2=中间时刻的瞬时速度

而匀变速直线运动的位移=平均速度×时间，故

利用位移公式和平均速度公式，得平均速度为

=

（2）利用微积分的基本定义可知，速度函数（关于时间）是位移函数的导数，而加速度函数是关于速度函数的导数，写成式子就是,

于是,就是初速度，可以是任意的常数

进而有 ,（对于匀变速直线运动），显然t=0时，s=0，故这个任意常数C=0，于是有

这就是位移公式。

(3)（代表相邻相等时间段内位移差，T代表相邻相等时间段的时间长度）

前一秒位移：

前两秒位移：

可计算出，前两秒位移之差为。此为从初速度为零的运动的推导，初速度不为零也可得到相同结论。

（4）

联立位移公式和速度公式，即可证明之。

二、速度公式推导

（1）中间位移的速度

证明：由位移公式，用换x可得到,

得到

再把代入到上式，可得

整理开平方后，即得

（2）中间时刻的速度

证明记为★式，记为●式

●式+★式，整理可得

把代入中，得到

比例关系

（1）重要比例关系

由，得。

由，得，或。

由，得，或。

（2）基本比例（当初速度为0的匀加速运动）

①第1秒末、第2秒末、……、第n秒末的速度之比

推导：

②前1秒内、前2秒内、……、前n秒内的位移之比

。

推导：

③第1个t内、第2个t内、……、第n个t内（相同时间内）的位移之比

推导：

④通过前1x、前2x、前3x……、前nx的位移所需时间之比

推导：,当位移等比例增大时，根号内的比值也等比例增大。

⑤通过第1个s、第2个s、第3个s、……、第n个s（通过连续相等的位移）所需时间之比

推导：

来源: 百度百科

内容资源由项目单位提供