含有两个未知数、且未知数对应项的次数为1的整式方程，叫作二元一次方程。单独的二元一次方程是不定方程，若干二元一次方程组成的方程组可能有唯一解。求解二元一次方程组一般采用消元法或克莱姆法则。

二元一次方程在几何上与平面中的直线是对应的。二元一次方程组的解在几何上是若干直线的交点。

二元一次方程在物理、化学等实际问题中有非常广泛的应用。

发展简史

二元一次方程的发展简史可以追溯到古代的数学问题，其中“鸡兔同笼”是最著名的问题之一。这个问题最早记录在《孙子算经》1中，时间大约在公元4世纪。2

线性方程组的研究在西方是由莱布尼茨在17世纪后期开创的。他研究了包含两个未知量的三个线性方程组。3到了18世纪，麦克劳林和克莱姆对线性方程组进行了研究，得到了如今的称为克莱姆法则的结果。克莱姆法则是在18世纪由法国数学家克莱姆发表的，它提供了一种当方程组的系数矩阵的行列式不为零时求解线性方程组的方法。3

高斯消元法是解线性方程组的一种重要方法，它通过行变换将方程组转化为上三角形式，然后依次回代求解。高斯消元法不仅可以用于求解线性方程组，还可以用于计算行列式、求矩阵的逆等。3

二元一次方程的发展经历了从实际问题抽象出数学模型，到形成系统的解法，再到算法的优化和广泛应用的过程。

定义

方程

含有两个未知数、且未知数对应项的次数为1的整式方程，叫做二元一次方程。45

设未知数为，常数，常数为实数，那么二元一次方程具有形式：

或形式：

方程组

把具有两个未知数的至少两个（很多时候恰为两个）一次整式方程所组成的一组方程，叫做二元一次方程组。45

设未知数为 ，常数，其中不同时为零，不同时为零，那么由两个方程构成的二元一次方程具有形式：

或形式：

二元一次方程组的解的情况有三种：无解、有唯一解、有无数个解。

二元一次方程组解法

使二元一次方程组中的各方程都成立的两个未知数的值，叫做该二元一次方程组的解。5

要使二元一次方程组有唯一解，至少需要两个方程。

下面将以解二元一次方程组

为例，给出两种解法。

消元法

利用两个方程中的其中一个，可以消去另一个方程中的一个未知数。

由两边同时乘，可得：

用减去该式，即可消去未知数，如下：

去分母后得：

由此解得：

最后将其代入即可得到的解为：

克莱姆法则快速求解

克莱姆法则是一种快速求解线性方程组的方法，对于由n个相容的方程组成的有唯一解的n元一次方程组，利用该法则可以直接得到方程组的解。

在二元情形下，该法则给出方程组的解为：

其中，的值由系数组成的行列式给出：36

计算举例

用上述方法，解二元一次方程组：

方法一：消元法

将第二个方程两边同时乘以2，再用第一个方程与之相减，得：

即：，解得。

代回原方程，得，从而解得。

于是原方程组的解为：

方法二：克莱姆法则

经计算得：

由克莱姆法则，立得原方程组的解为：

几何意义

代数式与几何图形之间有直接的关联。二元一次方程的几何意义，即为二维平面上的一条直线。

具体地，关于未知数的二元一次方程

与平面上的直线

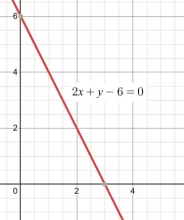
之间是一一对应的：一个方程唯一地确定的平面上的一条直线，一条直线也唯一地确定了一个方程。

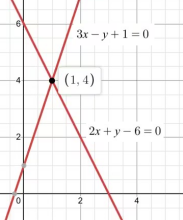容易观察到，直线上所有的点坐标均为对应二元一次方程的解，这从直观上解释了为什么仅由一个二元一次方程无法确定唯一的解。平面上的两条不平行、不重合的直线相交于一点，这对应了由两个二元一次方程组成的方程组有唯一解的情形。平面上两条直线平行，对应了方程组无解的情形。平面上两条直线重合，对应了方程组有无数个解的情形。

应用举例

二元一次方程组

例1 今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？17

译文：有若干只鸡和兔子被关在一个笼子里，从上面看，一共有35个头；从下面看，一共有94只脚。问笼子里鸡和兔各有多少只？

解：设鸡的只数是，兔的只数是，可知：

解之得

所以笼中有鸡23只，兔12只。

例2 两地相距280千米，一艘船在其间航行，顺流用14小时，逆流用20小时。求船在静水中的速度和水流速度。

解：设船在静水中的速度是（千米/时），水流速度是（千米/时），可知：

解之得

所以船在静水中的速度是17千米/时，水流速度是3千米/时。

例3 一定量的乙醇在氧气不足的情况下燃烧，生成。发生的化学反应方程式为：

和

如果16g的和

来源: 百度百科

内容资源由项目单位提供