均值不等式，又称基本不等式，是数学中一个非常重要的“恒不等式”1。它描述了对于任意两个正数，其几何平均值与算术平均值之间的关系，也可以推广到调和平均值和平方平均值构成一条不等式链。均值不等式有多种证明方法，可以推广至多元情形、幂均值不等式、矩阵不等式等，具有广泛的应用价值。

定理内容

二元情形

对于任意正数，有均值不等式1

其中，被称作两个正数的算术平均值（Arithmetic Mean，缩写为AM），被称作两个正数的几何平均值（Geometric Mean，缩写为GM），故该不等式又被称作“算术-几何均值不等式”。该不等式可以表述为：两个正数的算术平均值不小于它们的几何平均值。

该不等式又被称作“基本不等式”，这是由于其容易推广，得到其它各种不等式2。例如，用两个平方数来代换不等式中的，可以得到

该不等式对于任意实数都是成立的，且其被发现早于基本不等式2。

多元情形

均值不等式对任意有限个正数均成立。即对于任意正数，有3

类似地，是这些数的算术平均值，是这些数的几何平均值。

其它均值

除了算术平均值、几何平均值，还可以将其它的各种均值写入均值不等式。在二元情形下，对于两个正数，还有：

调和平均值（Harmonic Mean，缩写为HM）

平方平均值（Quadratic Mean，缩写为QM）

由基本不等式，可以将以上的平均值组成一条不等式链。该不等式链也被称为“均值不等式”：2

该不等式对任意有限个正数亦成立：

简写为：。表示个正数的调和平均值，不大于这个正数的几何平均值，不大于这个正数的算术平均值，不大于这个正数的平方平均值。如果在应用中观察到和、积、平方和、倒数和等类似的形式，可以考虑使用均值不等式。

除了这些平均值以外，对于两个正数，还有一个形式略不同的“对数平均值”（Logarithmic Mean）：

当时，对数平均值与其他平均值的关系为：

定理证明

二元情形

对于任意的两个正数，下面证明其算术平均值不小于几何平均值。

方法一：构造平方式

由于，当且仅当时等号成立。

将上式展开后移项立得，从而原不等式得证。

方法二：构造几何图形

早在4世纪，古希腊数学家帕普斯就在《数学汇编》中给出了下面的证明。4

如下图所示，在一个圆内接三角形中，是直径，是过点向边作的垂线，点是圆心。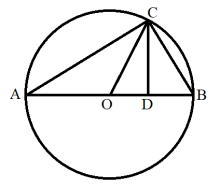

令，。

那么由圆的性质，可知。

由相似三角形，可知，从而。

从而由垂线段的性质即得，当且仅当重合（即）时取等号。

还可以过点作的垂线，垂足为，那么可以证明。由此，均值不等式中的调和平均值不大于几何平均值，也可以由几何图形直接说明。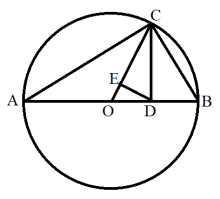

多元情形

对于任意正数的算术平均值与几何平均值，要证明均值不等式，可以考虑使用数学归纳法。

**方法一：**数学归纳法

假设已知下式对于成立：

那么可知对于也成立：

其中用到了三次已知条件，说明当且仅当时，即时等号成立。

而二元情形已证，故多元情形证毕。

来源: 百度百科

内容资源由项目单位提供