计算三角形面积的公式称为三角形面积公式。

同一平面内不共线的三点以及每两点连接的线段所组成的封闭图形(包括其内部)叫做三角形。1

三角形可以有不同的分类。按角分有直角三角形(三个角中有一个角是直角)，钝角三角形(三个角中有一个角是钝角)，锐角三角形(三个角全是锐角);按边分有等腰三角形(至少有两条边长是相等的)，等边三角形(三条边全部相等)。锐角三角形和钝角三角形统称为斜三角形。不同的三角形可以有不同的特殊形式的面积计算公式。

相关概念

三角形

平面上不共线的三点以及每两点连接的线段组成的封闭图形(包括其内部)叫做三角形,符号为，或者，也可以将不在同一条直线上的三条线段首尾依次相连形成的图形称为三角形，这两条定义等价。1

三角形有三个顶点，三条边，每条边都对应一条高，每个顶点处都有一条角平分线，每条边上都有一条中线(顶点与对边中点的连线)和高(顶点关于对边的垂线)。三角形的三条高，三条中线，三条角平分线，三条边的垂直平分线分别交于同一个点，称为垂心，重心，内心和外心。具体的可以在相关条目中查看。

如下图，在三角形中，把三点称为三角形的顶点，把三条线段称为三角形的边，把过点的与边所在直线的垂直的以点和垂足为端点的线段为在边上的高。

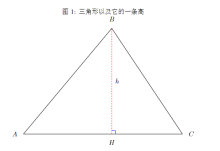
三角形可以使用不同的方法进行分类。按角分有直角三角形(三个角中有一个角是直角)，钝角三角形(三个角中有一个角是钝角)，锐角三角形(三个角全是锐角);按边分有等腰三角形(至少有两条边长是相等的)，等边三角形(三条边全部相等)。锐角三角形和钝角三角形统称为斜三角形。不同的三角形可以有不同的特殊形式的面积计算公式。

面积

"面积"是一个度量概念，用来衡量平面或曲面中"物体"的大小或者是三维空间中物体的表面的"大小"。一般而言规定边长为1单位长度的正方形的面积是1。

严格地说，面积是图形在两个不同方向上同时延展的可能性及程度在人脑中的反映而形成的概念。衡量物体表面或平面图形的大小的概念称为面积。平面图形的大小，是从这个平面图形占有的空间的范围大小的比较中产生的，因此表示平面图形大小的数量也是在比较中产生的。常选定一个正方形作为与平面图形比较的标准，并规定该正方形的面积为1，称为单位正方形。一个平面图形与单位正方形相比较之后所得的量数就是该平面图形的面积。

符号说明

如下图,

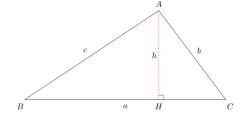
在下面的所有说明和证明中的记号和标记与此处的说明保持一致。

图中的大三角形的顶点附近有标记，将这三个点称为点，点，和点。那么就表示以符号中的标记对应的两个点为顶点的线段，在这张图中就分别对应三角形的三条边。

那么，这个三角形就可以用它的顶点来表示，把这个三角形记为，与顶点的记号相对应的小写字母(和,和,和)表示该顶点的对边，也可表示这条边的长度(如，可以表示边也可在计算中表示的长度；可以表示边，也可在计算中表示的长度；可以表示边，也可在计算中表示的长度。)

一般用来表示三角形的高，在这张图中这条高为线段，它是三角形的顶点对应的高，位于边上。点既是高的端点又是它和边的交点，也是它和边的垂足。注意，表示的不是的对边的边长，因为不是三角形顶点的标记。

如果在同一张图中出现不同的三角形，可以通过给标记加下标等方式标记不同三角形的高和它们的垂足来区分。

此外，表示角或者角的大小时，一般用符号表示，其中是角的顶点，和是角的两条边。在不会引起歧义的时候，可以把和省略，用表示以为顶点的角的大小.比如在这张图中，可以用来表示以和为边，为顶点的角的大小。类似的，表示以和为边，为顶点的角的大小。但是用在这张图中一般是不允许的，因为以为顶点的角有三个。

不过，在下面的证明和说明中，约定，表示，表示，表示，表示边

来源: 百度百科

内容资源由项目单位提供