十字相乘法是对二次多项式进行因式分解的方法之一。对于一个单变量的二次多项式，将其二次项系数与常数项进行因式分解，并按照一定的规则排列后，将其因数交叉相乘，如恰好得到一次项系数，则可以对其进行因式分解。这就是一般意义下的十字相乘法。对于多变量的二次多项式也有如“双十字相乘法”等类似的方法可以处理。

十字相乘法的特点是它要求使用者对多项式系数的因数分解与计算足够熟悉，而且该方法不一定可以求解任意的因式分解问题。这意味着便于用十字相乘法解决的因式分解问题较为有限。但是，在能够成功应用十字相乘法的情形下，该方法往往是十分高效快捷的。12

基于十字相乘法高效但不通用的特点，在目前的初中教学实践中，其去留仍有争议。

因式分解

因式分解是将多项式分解为几个整式的乘积的过程。

例如对于多项式，可将其分解为。

因式分解出的各整式的零点与原式的零点相同。例如的解为或，这与其因式分解后的结果是对应的。该结论建立起了因式分解与方程的根之间的关系：因式分解的结果可以有助于确定方程的根；方程的根可以有助于进行因式分解。

此外，高等代数中也有许多其它重要的与因式分解有关的结论。

方法过程与原理

此处讨论的十字相乘法关注的是形如（ 为常数，，）的二次多项式的分解。

原理与方法

考虑两个一次多项式相乘的过程

这说明如果能够从待分解的二次多项式中观察到有满足

那么就可以直接利用观察出的四个值来完成因式分解。因此，十字相乘法可以认为是一次多项式乘法的逆操作。

十字相乘法的具体步骤：

第一步，将二次项系数与常数项分解为两个数的乘积，即尝试性地寻找满足，的四个数：

第二步，将分解得到的四个数 “交叉相乘后相加” （如下图所示），检验此值是否与一次项系数 相同。此即“十字相乘法”名称的来源：

第三步，如果经检验得到的 与一次项系数 相同，那么可得 即为所求；反之如果不同，那么需要回到第一步，重新尝试分解 和 。这一步体现了十字相乘法并不能保证得到正确结果。

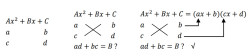
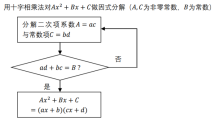上述步骤用流程图表示如图“十字相乘法流程图”：

可以注意到，上述流程图可能会在判断环节陷入死循环。这体现出十字相乘法不具备通用性——即并不是所有的二次多项式都便于用这种方法求解。

从竖式角度考虑原理

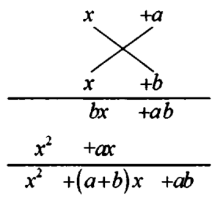一次多项式乘积也可以用“竖式”的角度去理解，如下图所示，展示了的竖式计算过程，从中也能看出“交叉相乘后相加”的步骤。

双十字相乘法

方法

双十字相乘法主要应对的是形如（）的二元二次多项式。其步骤与十字相乘法类似，但更复杂。

其步骤如下：

首先分解二次项系数中的以及常数项分别为

然后验证分解是否满足

如满足，则可以将原式因式分解为。

原理与推导

双十字相乘法本质上可以认为是将其中一个变量视为常数，例如：

若满足前述条件，则由十字相乘法可知，而且，于是再用一次十字相乘法即得：

这便是用十字相乘法推导双十字相乘法的过程。

应用举例

例1 因式分解：。

解：因为，且恰为一次项系数，

故。

例2 因式分解：。

解：因为，且恰为一次项系数，

故。

例3 因式分解：。

解：考虑以为一个整体，换元，则只需分解。

因为且恰为一次项系数，

故。

例4 因式分解：。

解：不妨此处将视作常数，那么：

因为，且恰为一次项系数，

故。

例5 因式分解：。

解：考虑以为一个整体，换元，则只需分解。

因为，且恰为一次项系数，

故。

例6 用双十字相乘法进行因式分解：。

解：因为，

且满足双十字相乘法的条件：

来源: 百度百科

内容资源由项目单位提供