三角形的重心是指三角形三条中线的交点。这个概念在平面几何的研究中具有重要的地位。对三角形重心的研究可以追溯到古希腊时期，阿基米德在《论平板的平衡》中对各种形状（包括三角形）物体的重心进行了讨论。1

在数学的研究中，随着时间的推移，重心的概念也被推广到了更高维度的空间中，可以在多维几何体中寻找重心。

重心的概念也被用于数学中的优化问题、物理学、工程学、计算机图形学等领域，用于计算图形的几何属性和物体的受力、稳定性等。

定义

三角形的三条中线交于一点，该交点称作三角形的重心。

可证明三角形的三条中线三线共点：取的中线，，令其交点为点，连接并延长于交于点。

由塞瓦定理2可知

解得，即点为边的中点。故三角形三条中线共点，该交点即为重心。

性质

性质定理1

重心到顶点的距离与重心到对边中点的距离之比为。

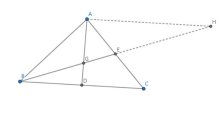
证明：过点作边的平行线交的延长线于点，则有

又由点是的重心可知，点是边的中点，即。

故代入比例关系可得

该性质定理得证。

性质定理2

重心与三顶点连线将三角形分为面积相等的三部分。重心到三条边的距离与三条边的长度成反比。

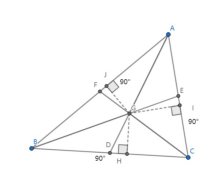
证明：由，是底边共直线的三角形可得

即。

同理可得，则两式相减可得到。

同理有，则有。

令，，，，，，则有

即

该性质定理得证。

性质定理3

点是的重心，则有向量关系。

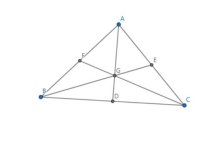
证明: 由点是的重心可知，点是边的中点，则有

由性质定理1可知，则有。

同理有。

因而

该性质定理得证。

在平面直角坐标系中，给出的顶点坐标，，，可依此解得其重心的坐标

性质定理4

重心到三角形各顶点的距离平方和最小。

证明：设在在平面直角坐标系中，的顶点坐标，，，考虑平面内任一点到三顶点距离平方和

来源: 百度百科

内容资源由项目单位提供