转动惯量（Moment of inertia）是经典力学中，刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度。转动惯量通常用字母I或J表示，其国际单位制单位为 kg·m²。1

转动惯量具有重要的物理意义，在转动力学中被用于方便地描述角动量、角速度、力矩和角加速度等数个量之间的关系，扮演着相当于质量在线性动力学中的角色。

在科学实验、工程技术、航天、电力、机械、仪表等工业领域中，刚体的转动惯量是一个重要的参量。如电磁系仪表的指示系统使用转动惯量不同的线圈，可分别测量微小的电流（检流器）或电量（冲击电流计）。在发动机叶片、飞轮、陀螺以及人造卫星的外形设计时，精确地测定转动惯量，也是十分必要的。

定义

一般定义

刚体每一无穷小区域都可以处理成点部位，所含质量记为，到转轴的垂直距离记为，速度为，角速度为定轴转动时刚体的动能为

也可表述成

其中I是由刚体物质分布和转轴位置确定的动力学量，称为刚体相对某转轴的转动惯量。1

转动惯量的量纲为，在国际单位制中，其单位为kg·m²

对于一个有多个质点的系统，。表示刚体的某个质元的质量，表示该质点到转轴的垂直距离。

对于刚体，可以对无限个质点的转动惯量求和，即用积分方法计算其转动惯量，，其中 是密度，是质点到转轴的距离。

张量定义

刚体绕某一点转动的惯性可由更普遍的惯性张量描述：

将刚体每一无穷小区域处理成点部位，刚体的动能为

（为了书写公式简便，此处和下文中省略了标记质点的下标）

将公式带入得（其中为刚体某点的速度，为刚体的质心速度，为刚体的转动角速度，为质点离质心的距离）

第二项可写成

由于，令，化简得

于是，刚体动能可以写成两个部分之和．第一项是平动的动能，其形式如同整个刚体质量集中在质心．第二项是刚体以角速度绕通过质心的轴转动的动能．

将转动动能改写成张量形式

(字母i, j, k表示张量的下标，可取值1,2,3．总是采用求和规则，按此规则省略求和号，在任何表示式中两次重复出现的下标——也称"哑"下标——就意味着对值1,2,3求和，例如,等等．显然"哑"下标的表示可以任意改变,只要它不与该式子中使用的其它下标相同)

这里用到了恒等式，其中 是单位张量（其分量在i = k时等于1，在i ≠ k时等于零）．引入张量

最终刚体动能表达式为

张量 称为刚体惯量矩张量，或者简称刚体惯量张量．

为了清楚起见，将惯量张量的分量写成显式

易知，它是对称的，即

分量称为对相应坐标轴的转动惯量．2

如果将刚体当作连续体，则在定义中的求和改为对刚体体积的积分：

像任何二阶对称张量一样，惯量张量可以通过适当选择坐标轴的方向约化为对角的形式．这些方向称为惯量主轴，而惯量张量相应的对角分量称为主转动惯量，用表示．在这样选择坐标轴时，转动动能表示为特别简单的形式：

相关定理

平行轴定理

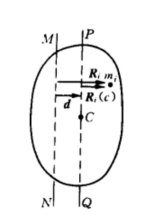
取两个互相平行、间距为的转轴MN和PQ，其中PQ过刚体质心C．对刚体任一质元，从MN轴设置径向朝外的矢量和，再从PQ轴向质元．引出矢量

如图所示．刚体相对MN 轴的转动惯量为

因

其中 应是PQ 轴向质心C 引出的矢量，自然为零．将刚体相对于过质心转轴PQ 的转动惯量记为

则有

其中为刚体质量，这就是刚体转动惯量的平行轴定理。1

垂直轴定理

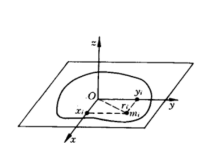
以平板刚体某一点部位为坐标原点建立坐标系，使板平面恰好在平面上，如图5-18所示．将刚体相对于轴的转动惯量分别记为则有

即

来源: 百度百科

内容资源由项目单位提供