拉格朗日中值定理,又称拉氏定理、有限增量定理,是微分学中的基本定理之一,反映了可导函数在闭区间上整体的平均变化率与区间内某点的局部变化率的关系。
定理的现代形式如下:
如果函数f(x)满足:
(i)在闭区间上[a,b]连续;
(ii)在开区间(a,b)上可导;
那么在开区间(a,b)内至少存在一点ξ使得f'(ξ)=(f(b)-f(a))/(b-a)。14818
拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一阶展开)。
1797年,拉格朗日中值定理由法国数学家约瑟夫·拉格朗日在《解析函数论》中首先提出,并提供了最初的证明。现代形式的拉格朗日中值定理由法国数学家O.博内提出。1
拉格朗日中值定理沟通了函数与其导数的联系。在研究函数的单调性、凹凸性以及不等式的证明等方面,都可能用到拉格朗日中值定理。6
定理内容
定理表述
最初形式
函数![]() 在
在![]() 和
和![]() 之间连续,
之间连续,![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() 必取
必取![]() ,
,![]() 中的一个值14。
中的一个值14。
现代形式
如果函数![]() 在闭区间
在闭区间![]() 上连续,在开区间
上连续,在开区间![]() 上可导,那么在开区间
上可导,那么在开区间![]() 内至少存在一点
内至少存在一点![]() 使得
使得![]() 14。
14。
结论变形
拉格朗日中值定理的结论有几种变形:![]() 或令
或令![]() ,
,![]() ,
,![]() ,有
,有![]()
若把![]() 记成
记成![]() ,则
,则![]()
上面第一式称为拉格朗日中值公式,第二式和第三式称为有限增量公式。
拉格朗日中值定理也称为有限增量定理,视其重要性,又称为微分中值定理2。
推导验证
下面依据罗尔中值定理,通过构建辅助函数(F(x)),推导拉格朗日中值定理的证明过程。
设![]() ,由于
,由于![]() 在闭区间
在闭区间![]() 上连续,在
上连续,在![]() 内可导,因此
内可导,因此![]() 在闭区间
在闭区间![]() 上连续,在
上连续,在![]() 内可导。
内可导。
又![]() ,所以根据罗尔中值定理,在
,所以根据罗尔中值定理,在![]() 内至少存在一点
内至少存在一点![]() ,使
,使![]() 亦即
亦即![]() 或
或![]()
以上证明是在![]() 的情况下得到的,如果
的情况下得到的,如果![]() ,同样可证得定理的结论318。
,同样可证得定理的结论318。
发展历程
人类对微分中值定理的认识始于古希腊时代。当时的数学家们发现,过抛物线顶点的切线必平行于抛物线底端的连线,阿基米德还利用该结论求出了抛物线弓形的面积。这其实就是拉格朗日中值定理的特殊情形。
1635年,意大利数学家博纳文图拉·卡瓦列里在《不可分量几何学》中描述:曲线段上必有一点的切线平行于曲线的弦,即卡瓦列里定理。它反映了微分中值定理的几何形式。
1637年,法国数学家皮耶·德·费马在《求最大值和最小值的方法》中给出了费马定理,即函数在极值点处的导数为零。
1691年,法国数学家米歇尔·罗尔在《方程的解法》中给出了多项式形式的罗尔中值定理,后来发展成一般函数的罗尔定理,并且正是由费马定理推导而出。
1797年,法国数学家约瑟夫·拉格朗日在《解析函数论》中首先给出了拉格朗日中值定理,并予以证明。它也是微分中值定理中最为主要的定理。
19世纪10年代至20年代,法国的数学家奥古斯丁·路易斯·柯西对微分中值定理进行了更加深入的研究。他的三部巨著《分析教程》《无穷小计算教程概论》和《微分计算教程》,在分析上进行了严格的叙述和论证,对微积分理论进行了重构。他在《无穷小计算教程概论》中严格地证明了拉格朗日中值定理,后来又在《微分计算教程》中将拉格朗日中值定理推广为广义中值定理——柯西中值定理。
现代形式的拉格朗日中值定理是法国数学家O.博内在其著作《Cours de Calcul Differentiel et integral》中提出的,他并非利用![]() 的连续性,而是利用了罗尔中值定理对拉格朗日中值定理加以重新证明1。
的连续性,而是利用了罗尔中值定理对拉格朗日中值定理加以重新证明1。
定理推广
学术意义
几何意义
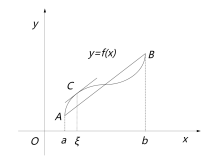 若连续曲线
若连续曲线![]() 在点
在点![]() ,
,![]() 之间的每一点处都有不垂直于
之间的每一点处都有不垂直于![]() 轴的切线,则曲线在
轴的切线,则曲线在![]() 、
、![]() 间至少存在一点
间至少存在一点![]() ,使得该点处的切线与割线
,使得该点处的切线与割线![]() 平行。45
平行。45
运动学意义
对于曲线运动,在任意一个运动过程中至少存在一个位置(或一个时刻)的瞬时速率等于这个过程中的平均速率。45
推理推论
根据拉格朗日中值定理,可以得到下列推论:
推论1:若函数![]() 在区间
在区间![]() 上的任意点
上的任意点![]() 处的导数
处的导数![]()
来源: 百度百科
内容资源由项目单位提供


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助
 百度百科
百度百科 