指数函数是重要的基本初等函数之一，其定义来源于正整数指数的运算。指数函数作为一元实函数时，其表现出的特点与底数有关；作为一元复函数时，指数函数是一个单值的在复平面处处解析的周期函数。

指数函数具有广泛的应用。它可以用于描述复制增殖的生物过程、算法的计算复杂度等。

指数运算

正指数运算

当为正整数时，个数的积可记作，又称的次方。其表达式为

整数指数

当且时， 。

当且时，。

分数指数

当为最简分数形式，为正整数且时，。

其中表示的次方根，其为关于的方程的唯一正实数解。1

实数指数

当且时，考虑集合满足

故对于任意满足的有理数，可知是的上界。根据确界原理，可知集合存在上确界，由此定义

当且时，。

当且时，。1

至此，可以得到定义在实数上的一元实值函数。

函数图像和性质

指数运算的性质

正整数指数的上述性质可以很容易验证。可以认为，有理数指数的定义是为了保持正整数指数的上述性质而给出的，实数指数的定义是为了使得指数函数连续而给出的。

指数函数的图像

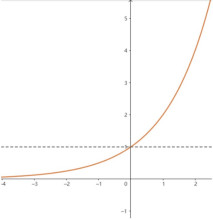
当时，函数的图象大致如图。

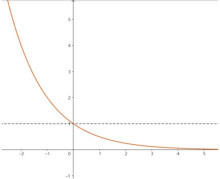
当时，函数的图象大致如图。

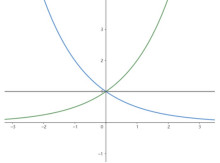
当两正数满足时，函数和的图象关于y轴对称。

指数函数的性质

指数函数的定义域为，值域为。

指数函数在处的取值等于，与的具体取值无关。即。

当时，指数函数在单调递增。且当时，；当时，。

当

来源: 百度百科

内容资源由项目单位提供