通过表面的磁通量是表面上磁场B的沿法线方向的分量与表面积的积分，通常表示为Φ。磁通量的定义的数学表达式是

Φ=∫SB·dS (1)

磁通量的量纲是ML2T**-2I-1。磁通量的单位在国际单位制中是韦伯（Wb），在高斯单位制中是麦克斯韦（maxwell），单位换算是1maxwell=10-8Wb。

基本公式

高斯定理

磁通量的高斯定理是麦克斯韦方程组之一，它说的是穿过闭合曲面的总的磁通量是零。数学表达式是

(2)

或者写成微分形式

(3)

在现有的理论中，磁场是无源场，也就是说磁单极子不存在。在实验中尚未发现磁单极子，但是理论上不排除磁单极子存在的可能性电动势。

电动势

法拉第发现，通过导线环路磁通量的变化会引起环路中产生电动势，法拉第定律是

（4）

其中是电动势。在麦克斯韦方程组中，这个公式常被写成微分形式

(5)

电动势的定义详见词条电动势。

与磁矢势的关系

磁矢势的定义是，将这个公式代入磁通量的定义，应用斯托克斯公式，可以得到磁矢势与磁通量的关系

(6)

其中积分环路对应着计算磁通量时考虑的面积的边界。

磁通量子化

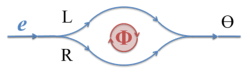考虑一个方向的匀强磁场，，这个磁场的范围是半径为的一个圆。要产生这个磁场所需的磁矢势是，其中是角度方向的单位矢量。电磁相互作用对作用量的贡献是

(7)

因此，根据量子力学中的路径积分公式，电子从运动到的过程中，磁场会导致波函数改变一个相位

(8)

其中是沿着电子运动路径积分的微元。我们从电磁学理论中可以知道，的线积分与路径无关。也就是说只要一对不同路径形成的圈没有包围磁通量，那么这个积分仅依赖于两个端点。因此，当我们计算从到所有路径对跃迁振幅的贡献时，图中在磁通量上面的轨迹对路径积分的贡献都可以用同一个相位因子来表示,对于在磁通量下面的轨迹也是如此。对于经过路径或从路径的粒子，磁通量会使其产生一个相位差

(9)

这意味着当我们改变磁场强度时，在图中区观测到粒子的概率中存在一个正弦分量，周期由磁通量基本单位给出

(10)

这个相位会导致带电粒子经过磁通量后波函数会发生干涉，形成实验中可以观测的干涉条纹。这就是阿哈罗诺夫-玻姆效应（Aharonov-Bohm effect）的实验。

发展历史

磁通量是研究磁现象时的一个辅助物理量，并不是一个基本的物理量，因此在物理理论的发展中并不受重视。

1831年迈克尔·法拉第（Micheal Faraday）发现了电磁感应，并提出了法拉第电磁感应定律。在法拉第电磁感应定律中，磁通量的改变会引起回路中的电动势。

1949年，维尔纳·艾伦伯格（Werner Ehrenberg）和雷蒙德·埃尔德雷德·西迪（Raymond Eldred Siday）预言了阿哈罗诺夫-玻姆效应（Aharonov-Bohm effect，简称AB效应）。1959年亚基尔·阿哈罗诺夫（Yakir Aharonov）和大卫·玻姆（David Bohm）发表了他们对AB效应研究的论文。AB效应可以推导出磁通量的量子化1。

来源: 百度百科

内容资源由项目单位提供