HL定理（英文：HLtheorem）是判定两个直角三角形全等的定理。该定理通过判定两个直角三角形的斜边和一条直角边对应相等来判定两个直角三角形全等。

该定理是两个三角形“边边角”（SSA）的特殊情况，即三角形的两边和其中一边的对角分别相等的两个三角形全等。直角三角形可以通过勾股定理转化为“SSS”或“SAS”。一般三角形不可以用“边边角”（SSA）判定两个三角形全等。

定理内容

斜边和一条直角边分别相等的两个三角形全等（可以简写成“斜边、直角边”或“HL”）。1

定理条件

为什么一般三角形不能用“SSA”判定全等

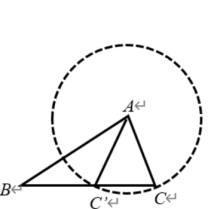
如图1，固定AB的长度和∠B的大小，以A为圆心，AC(AC>ABsinB)长为半径作圆。这个圆交直线BC于另一点C’。在△ABC和△ABC’中，AB=AB，∠B=∠B，AC=AC’，满足“SSA”的条件，但是∠ACB≠∠AC’B，△ABC和△ABC’不全等。由AC=AC’和等边对等角，∠ACB=∠AC’C，因此∠*ACB+∠AC’B=∠AC’C+∠AC’B=*180°。

虽然“SSA”不可以作为三角形全等的判定依据，但是特定三角形下，“SSA”也可以保证两个三角形全等。比如满足“SSA”的两个锐角三角形全等，以及满足“SSA”且对角均为钝角的两个钝角三角形全等。2

HL定理的适用条件

由图1可知，△ABC和△ABC’不全等。但是如果将AC的长度缩短，C’点与C点的距离就会缩短，直到C’点与C点重合，此时对应∠ACB=90°即△ABC是直角三角形。这时只需要AB=AB和*AC=AC’*就可以判定全等了。

HL定理适用于两个直角三角形全等的判定，其中H是hypotenuse（斜边）的缩写，L是leg（直角边）的缩写。

定理证明

证法（1）

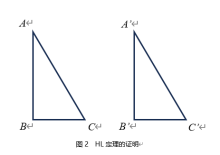如图2，在Rt△ABC和Rt△*A’B’C’*中，

∠B=∠B’=90°AB=A’B’ AC=A’C’ ,

证法（2）

如图3，平移ΔA'B'C'使得A'与A重合，B'与B重合由∠ABC=∠A'B'C'=90°可知∠ABC+∠A'B'C'=180°因此三点C,B(B'),C'在同一直线上

来源: 百度百科

内容资源由项目单位提供