伽玛函数（Gamma函数），一般用希腊字母Γ表示，也叫第二类欧拉积分。 伽玛函数是阶乘函数在实数与复数上延拓的一类函数，但并不是唯一的。它在除了非正整数外的整个复数域都有定义。

对于每一个正整数n，满足Γ(n)=(n-1)!。

该函数在分析学、概率论、偏微分方程和组合数学中有重要的应用。与之有密切联系的函数是贝塔函数（Beta function），也叫第一类欧拉积分。

引言

伽玛函数的理论源自于阶乘函数的推广问题，即找到一个函数，使得只对自然数n有定义的阶乘函数可以延拓到实数（甚至复数）域上，这样我们就可以自然地定义的值。

在寻找这样的表达的过程中，我们遇到了以下众所周知的不恰当之处：欧拉发现当n为整数时，有1

这意味着我们可以将整数n替换成任意的正实数（保证积分的收敛性）x并定义。

然而，阶乘函数的推广问题本质上是一个插值问题，这意味着阶乘有无限多种的连续扩张方式将定义域扩张到非整数，理由是可以对任何一组孤立点画出无限多的曲线。后来证明伽玛函数是最好的一个选择（它是满足一系列拥有好的性质的函数的唯一解）。然而，它并不是唯一一个扩张阶乘意义的解析函数。

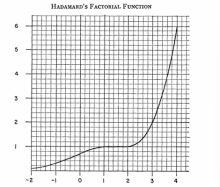例：阿达玛阶乘函数（Hadamard’s factorial function）是一个相对于伽玛函数十分简单的函数，它在正整数处与伽玛函数重合，且在整个复平面上不存在奇点 2：

定义

主定义

的记号是由勒让德（Legendre）提出的2，当复数s的实部严格大于0时（即），伽玛函数定义为积分

这个积分（也叫第二类欧拉积分）在时收敛。于是伽玛函数的定义域为半平面1。

欧拉的定义

欧拉的定义表现为无穷乘积的形式。欧拉在研究无穷乘积时意识到，当n是正整数时，有 2

这个无穷乘积如今更常规地写成

这个无穷乘积对除了非正整数以外（在非正整数处由于要把0作为分母而无意义）的所有都有定义。1

威尔斯特拉斯的定义

威尔斯特拉斯（Weiersteass）对伽玛函数的定义适用于除了非正整数以外的所有复数s 1:

事实上这个定义是由的阿达玛无穷乘积形式取倒数得到的，关于这个形式的细节部分见伽玛函数的倒数一节。

威尔斯特拉斯的定义的好处是我们可以用这个形式直接定义对数伽玛函数3

关于这个函数的细节部分将在对数伽玛函数一节说明。

解析延拓

定义在上的可以解析延拓为复平面ℂ上的一个亚纯函数，其奇点仅出现在非正整数上。

考虑

其中定义了一个整函数（保证了积分的收敛性），现在考虑，将展开成泰勒级数并交换积分与求和顺序（这一步需要验证，但并不困难），得到

于是当时，

这一级数可以自然延拓为复平面ℂ上的亚纯函数1。

性质

一般性质

a.伽玛函数满足递推公式。

这个方程是伽玛函数几乎所有其他理论的发展基础。特别地，因为。我们推出，当时，有

反复应用递推公式可以直接推出：

b.余元公式（也叫欧拉反射原理，Euler’s reflection formula）

当时，称Γ函数的自变量s与1-s是互余的，因此等式

叫作Γ函数的余元公式。

特别地，令，可以直接由余元公式推出 。

c.光滑性和导数形式

伽玛函数是无限次可微的，且其n阶导数为

d.欧拉-高斯公式

通常称下面的等式

为欧拉-高斯公式。事实上这一公式就是欧拉对伽玛函数的定义4。

不等式

当时，伽玛函数是严格的对数凸函数，于是我们有

或者其等价形式

这个不等式可以通过对数伽玛函数的导函数得到证明，关于对数伽玛函数及其导数形式可以见对数伽玛函数一节3。

斯特林公式

将函数

表示成拉普拉斯积分的形式：

而且如果在时做变量替换，则化成积分

函数在区间上有唯一的极大值点，且 ，根据拉

来源: 百度百科

内容资源由项目单位提供