方差是刻画随机变量在其中心位置附近散布程度的数学特征，反映了随机变量取值的离散程度12，常用的符号有σ²，s²，Var(X)，D(X)等1。

对于一个服从分布F的随机变量X，其方差定义为Var(X)=E[(X-μ)2]，其中E(X) 表示X的期望（即均值 ）。这个定义适用于所有类型的随机变量，包括连续和离散分布等。

方差提供了衡量数据在平均值附近波动程度的方法：方差越大，数据分布越分散，波动越大；方差越小，数据越集中，波动越小。为了消除偏差带来的正负抵消，方差通过对偏离均值的差值进行平方后取期望的方式，达到了衡量数据散布程度的目的。

方差（variance）这个名词率先由罗纳德·费希尔（Ronald Fisher）在1918年发表的论文《孟德尔遗传假定下的亲缘之间的相关性》(《The Correlation between Relatives on theSupposition of Mendelian Inheritance》3)中提出。

历史

方差（variance）这个名词率先由罗纳德·费希尔（Ronald Fisher）在1918年发表的论文《孟德尔遗传假定下的亲缘之间的相关性》(《The Correlation between Relatives on the Suppositionof Mendelian Inheritance》3)中提出。

到了20世纪30年代，行为科学家开始采用方差分析方法，但其普及进程相对较慢。随着二战结束后科学研究的繁荣，行为和心理科学快速发展，方差分析被使用得越来越频繁。这一时期科学界对统计显著性检验的重视也进一步推动了方差分析的应用，方差分析逐渐成为行为科学家们验证实验结果有效性和确保研究科学性的关键工具之一4。

定义

方差是刻画随机变量在其中心位置附近散布程度的数学特征，反映了随机变量取值的离散程度12，常用的符号有，，，等1。

设为服从分布的随机变量，如果是随机变量的期望(记均值)，则随机变量（或分布）的方差 为1：

这个定义涵盖了连续、离散，或两者皆非的随机变量。

方差的表达式可展开如下：

即 ，方差的这个形式在计算上往往较为方便1。

方差也可以视作随机变量与自身的协方差：

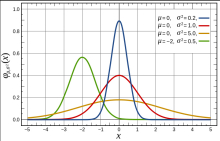
方差计算方法

方差一般可由定义

直接算出。根据随机变量是离散型的还是连续型的，方差的计算公式有不同的形式。

离散型随机变量

设 为离散型随机变量，且数学期望存在。

若

则称为 的方差。

将上式展开后可得

连续型随机变量

设为连续型随机变量，其密度函数为，且数学期望存在，则

称为的方差。

将上式展开后可得

矩生成函数计算

在概率论和统计学中，矩生成函数（Moment Generating Function，简称MGF）是一个随机变量的一个重要特征函数，用来生成其矩。对于随机变量 ，假设它的矩生成函数存在，则其矩生成函数定义为3：

矩生成函数 可以在 附近的某个区间内展开成幂级数：

该展开式中各项的系数为的矩，因此矩生成函数在 处的导数可以提供随机变量的矩信息。利用矩生成函数 计在处的前几阶导数，可以得到均值 和二阶矩 ，从而计算方差。

具体步骤如下：

1.计算均值：均值可以通过矩生成函数的导数在 处求得：

2.计算二阶矩 ：二阶矩可以通过矩生成函数的二阶导数在 处求得：

3.计算方差：利用方差的定义

可以得到

意义

方差用于刻画随机变量在其中心位置附近散布程度的数学特征。当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小5。

设随机变量有均值 。试验中，取的值不会恰好为a，而会有所偏离，而偏移的量本身也是随机的。我们要找到一个量来刻画这个偏离，就不能取的均值，因为，即正负偏离彼此抵消了。一种解决办法是取的绝对值

来源: 百度百科

内容资源由项目单位提供