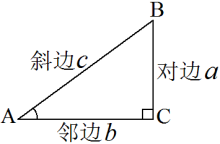
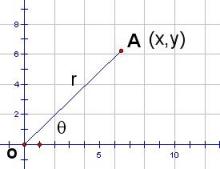
三角函数是数学中属于初等函数中的超越函数的函数，它的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中利用单位圆来定义的，其定义域为整个实数域。另一种定义建立在直角三角形边角关系的基础上，但并不完备。现代数学把它们描述成无穷数列的极限和微分方程的解，并将其定义扩展到复数系。

尽管三角函数的公式种类繁多，如和差角公式、倍角公式、辅助角公式等，但只要掌握了三角函数的本质及内部规律，就会发现三角函数各个公式之间有紧密的联系。例如，诱导公式之间可以互相推得，而倍角和半角公式则是和差角公式的特殊形式。掌握三角函数的内部规律及本质是学好三角函数的关键所在。

三角函数具有许多优美的性质，使其能够广泛应用于物理、工程、信号处理等领域中，成为许多复杂问题的解决方案。

定义式

锐角三角函数的定义建立在三角形的边和角之间关系的基础上，将直角三角形的内角和三角形的边长比值相关联；利用单位圆的各种有关线段的长来定义，则可以把锐角三角函数推广到任意角三角函数8。


锐角三角函数

任意角三角函数

图形

正弦函数（sin）

余弦函数（cos）

正切函数（tan）

余切函数（cot）

正割函数（sec）

余割函数（csc）

注：正切函数、余切函数曾被写作tg、ctg，现已不用这种写法。

参考资料来源：现代汉语词典1。

函数

定义域

值域

周期

sinx

(-∞,+∞)

[-1,1]

2π

cosx

(-∞,+∞)

[-1,1]

2π

tanx

(-∞,+∞)\{π/2+kπ|k∈Z}

(-∞,+∞)

π

cotx

(-∞,+∞) \{kπ|k∈Z}

(-∞,+∞)

π

secx

(-∞,+∞) \{π/2+kπ|k∈Z}

(-∞,-1]∪[1,+∞)

2π

cscx

(-∞,+∞) \{kπ|k∈Z}

(-∞,-1]∪[1,+∞)

2π

函数关系

倒数关系：①；②；③。

商的关系：①；②。

平方关系：①；②；③。

诱导公式

公式一：设为任意角，终边相同的角的同一三角函数的值相等：

公式二：设为任意角，与的三角函数值之间的关系：

公式三：任意角与的三角函数值之间的关系：

公式四：与的三角函数值之间的关系：

公式五：与的三角函数值之间的关系：

公式六：及与的三角函数值之间的关系：

记忆方法：奇变偶不变，符号看象限

形如的角，“奇、偶”指的是的奇偶，“变与不变”指的是三角函数的名称的变化：“变”是指正弦(sin)变余弦(cos)，正切(tan)变余切(cot)（反之亦然成立）。“符号看象限”的含义是：当角为锐角时，看是第几象限角；若所在象限的角使该三角函数值为负数，则等式右边为负号；反之为

来源: 百度百科

内容资源由项目单位提供