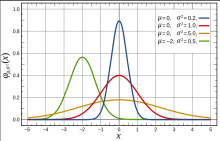
正态分布（Normal distribution），又称为常态分布或高斯分布，通常记作X~N（μ ,σ2）。其中， μ是正态分布的数学期望（均值）， σ2是正态分布的方差。μ = 0,σ = 1的正态分布被称为标准正态分布1。22

正态分布的概率密度函数显示为典型的钟形曲线，这一形状类似于寺庙中的大钟，因此也常被称为钟形曲线。作为一种连续分布，正态分布拥有完备的概率密度函数、累积分布函数、矩生成函数和特征函数等表达形式，并且具备明确的期望（即均值）、方差、偏度和峰度等数值特征。中心极限定理阐述了在一定条件下，多个独立同分布的随机变量的平均值会趋向于正态分布，这一现象在样本量增大时尤为显著2。

正态分布，最初由法国数学家棣莫弗（A. D. Moivre）在1733年引入3，最初的探索并未深入其在统计学上的应用，尤其是在误差分析方面。随后，高斯（C. F. Gauss）提出了关于“正态误差”的理论，并与拉普拉斯（P-S.Laplace）共同深入研究了正态分布的各项特性。

在现实世界中，许多自然和社会现象如考试成绩和人体身高等，都近似遵循正态分布。这种分布是统计分析和概率论中的核心概念，广泛应用于诸如质量控制、频数估计以及制定医学参考标准等领域2。正态分布在统计学领域具有深远的意义。

定义

概率密度函数

如果一维随机变量的密度函数为：

其中和为常数且，则称随机变量服从参数为的正态分布，记作1，读作X服从。为总体均数，为总体标准差4。这里N为”Normal distribution(正态分布)”一词的首字母5。

特别地，当时，正态分布称为标准正态分布，其密度函数为：

标准正态分布之所以重要，一个原因在于：任意的正态分布的计算很容易转化为标准正态分布。容易证明：若，则5。

累积分布函数

累积分布函数，也叫分布函数，是概率密度函数的积分。概率密度函数与分布函数是一一对应的，即知道其一即可求出另一个5。根据连续型随机变量分布函数的定义，一般正态分布的分布函数为：

特别地，当参数时，标准正态分布的分布函数为

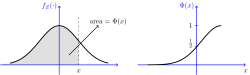
且有。

图形特征

正态分布可以通过一系列矩（moments）逐步揭示其图形特征，包括位置、离散程度、对称性和尾部特性。矩是关于随机变量的期望值的函数，用于描述分布的几何和统计特性。设为随机变量，c为常数，k为正整数，则称为关于c点的k阶矩。

均值

均值是分布的一阶原点矩，定义为。对于正态分布，均值描述了分布的中心位置，即钟形曲线的对称轴所在的位置。在标准正态分布中，均值为0。正态分布是对称的，因此均值也是分布的众数和中位数。

方差

方差是分布的二阶矩，定义为

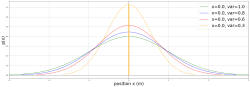
它描述了随机变量相对于均值的平均偏离程度。对于正态分布，方差决定了分布的宽度或离散性。较大的方差意味着分布较为分散，曲线更为平坦；较小的方差意味着分布更为集中，曲线更为尖锐。

固定的值不变，改变的值，则曲线的位置不变，但随着的减小，曲线变得陡峭4。

偏度

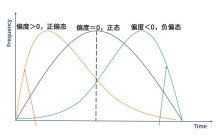
偏度，也称偏度系数，是用来衡量统计数据分布的偏斜方向和程度的指标6。偏度定义为：

偏度描述了概率分布密度曲线相对于平均值的不对称性。

当时，表示数据分布完全对称，左右尾部长度相等，例如正态分布的偏度即为06。时,称分布为正偏，较多的数据值偏离了平均值向左侧集中；时，称分布为负偏，较多的数据值偏离了平均值向右侧集中7。若显著异于0，则说明分布与正态有较大的偏离。

峰度

峰度是描述数据分布形态陡缓程度的统计量，峰度越大，数据分布越陡峭，尾部越厚；峰度越小，数据分布越平滑6。峰度的计算公式为

正态分布的峰度为3，很多情况下，为方便计算，一般将正态分布的峰度值减去3，这样使得其峰度变为0，更方便进行比较。当数据的峰度为0时，表示数据分布的陡缓程度与正态分布相同；峰度大于0，表示数据分布比正态分布更陡峭，而峰度小于0，表示数据分布比正态分布更平坦；峰度的绝对值越大，表示数据分布形态与正态分布的差异越大6。

性质

无限可分性

当多个随机变量相互独立且服从正态分布时，它们的线性组合仍然服从正态分布。具体而言，如果有一组独立同分布的随机变量，其中每个变量均服从正态分布，那么对于任意实数系数，其线性组合也服从正态分布。

在线性组合下，加法和标准乘法保持不变8。例如，如果且是统计独立的正态随机变量，那么它们的和

也服从正态分布。同样，它们的差也服从正态分布：

如果与两者是相互独立的，则与的方差相等9。

最大熵

随机变量的概率密度函数为，当期望和方差分别为：

来源: 百度百科

内容资源由项目单位提供