泊松分布（Poisson distribution），又称波哇松分布、卜瓦松分布，是一种重要的离散型分布。

若随机变量 X 服从参数为λ的泊松分布，其中 λ > 0，则记为X~π(λ)，或记为X~Possion(λ) 。在泊松分布中，λ是唯一的参数，它既是数学期望也是方差1。

泊松分布可作为二项分布的极限而得到。若二项分布的试验次数n很大，二项分布的概率p很小，且乘积 λ=np比较适中，则事件出现的次数的概率可以用泊松分布来逼近2。

1837年，法国数学家西莫恩·德尼·泊松（Siméon-DenisPoisson）首次提出泊松分布的概念3。

泊松分布在实际中有着广泛的应用，它常与单位时间或单位面积及单位产品上的计数过程相联系4，例如汽车站台的候客人数、机器出现的故障数、DNA序列的变异数等。

定义

泊松分布是一种重要的离散型分布。如果离散型随机变量 X 可取一切非负整数值，且有

则称 X 服从参数为 λ 的泊松分布，其中 λ > 0，记为，或记为 。泊松分布的平均值 m= λ，方差 = λ 25。

与二项分布的联系

在二项分布的伯努利试验中，如果试验次数n很大，二项分布的概率p很小，且乘积 λ=np比较适中，则事件出现的次数的概率可以用泊松分布来逼近2。在这种条件下，将较难计算的二项分布近似为泊松分布去计算较为方便25。

泊松定理指出，在独立试验中，以代表事件 A 在试验中出现的概率，它与试验总数有关。如果，当时，二项分布的极限为泊松分布6。下面给出证明。

记 ，为二项分布，则：

对给定的，有：

及

因此：

泊松分布公式为：

其中是泊松分布的参数6。

性质

方差与期望

在泊松分布中，唯一的参数既是数学期望也是方差。推导如下：

设随机变量 ，则

这表明泊松分布的数学期望就是参数。

又因为

由此得的方差为

也就是说，泊松分布的方差与数学期望均为。

可加性

两个独立且服从泊松分布的随机变量，其和仍然服从泊松分布。即若且，则。

特征函数

泊松分布的特征函数为。

其他性质

(1)泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件，样本含量必须很大18。

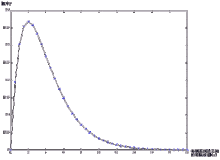
(2)是泊松分布所依赖的唯一参数。值愈小，分布愈偏倚，随着增大，分布趋于对称18。

(3)当=20时分布泊松分布接近于正态分布；当=50时，可以认为泊松分布呈正态分布。 在实际工作中，当20时就可以用正态分布来近似地处理泊松分布的问题18。

参数估计

最大似然估计

对于泊松分布，假设有n个观测值，它们都是独立同分布的随机变量，服从参数为的泊松分布。泊松分布的似然函数为：

为了简化计算，通常对似然函数取对数：

关于求导并令其等于 0，可以得到最大似然估计值：

即泊松分布的参数的最大似然估计值就是观测样本的均值7。

贝叶斯估计

由贝叶斯公式知，在给定事件的情况下，事件A的条件概率与事件在给定事件发生的条件下的条件概率的关系如下：

结合全概率公式，贝叶斯公式可以进一步表示为：

贝叶斯估计的步骤如下：

1. 给定先验分布

来源: 百度百科

内容资源由项目单位提供