开普勒定律（英语：Kepler'slaw）是由德国天文学家兼数学家约翰尼斯·开普勒所发现的、关于行星运动的定律，由三条子定律所组成。开普勒于1609年在他出版的《新天文学》科学杂志上发表了关于行星运动的两条定律，又于1618年，发现了第三条定律。这些定律用椭圆轨道取代了尼古拉·哥白尼日心说中的圆形轨道和本轮，并解释了行星速度的变化情况，三条子定律大致为1：

第一定律：行星的轨道是一个以太阳为焦点之一的椭圆；

第二定律：行星和太阳之间的连线在相等的时间间隔内扫过相等的面积；

第三定律：行星轨道周期的平方与其轨道半长轴的立方成正比。

在天文学与物理学上、开普勒的定律给予亚里士多德派与托勒密派极大的挑战，这些论点大大地动摇了当时的天文学与物理学。经过几乎一个世纪的研究，物理学家终于能够运用物理理论解释原理。艾萨克·牛顿于1687年，应用他的第二定律和万有引力定律，在数学上严格地证明了开普勒定律。

更精确的历史方法可参见《新天文学》和《哥白尼天文学纲要》。

开普勒第一定律

开普勒第一定律的内容

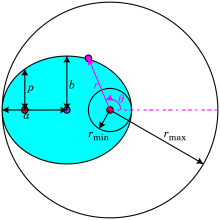
内容：行星的轨道都是一个以恒星为焦点之一的椭圆。

椭圆具有两个焦点，在太阳系中，太阳就位于行星椭圆轨道的其中一个焦点上。以太阳为中心的极坐标系统用于描述行星相对于太阳的运动关系，在数学上，椭圆可以用公式表示：

其中是半通径，是椭圆的离心率，是行星到太阳的距离（日心距），是以太阳为观察点，从近日点开始测量的行星当前位置的角度。

对于椭圆，；在极限情况下，，轨道是一个以太阳为中心的圆（即偏心率为零），而当时，行星位于远日点（冬至点），日心距达到最小值：

当时，行星位于春分点或秋分点，此时日心距为。

当时，行星位于远日点（夏至点），此时日心距达到最大值，

半长轴是和的算数平均数，

半短轴是和的几何平均数，

半通径是和的调和平均数，

离心率是和的变异系数，

椭圆的面积为；特殊情形下，时，椭圆变为正圆，有：

开普勒第一定律的数学证明

设定，则角速度为：

对时间微分和对角度微分有如下关系：

根据上述关系，径向距离对时间的导数为：

再求一次导数：

代入径向运动方程，有：

将此方程除以，则可得到一个简单的常系数非齐次线性全微分方程来描述行星轨道：

为了解这个微分方程，先列出一个特解：

再求解剩余的常系数齐次线性全微分方程：

其解为，这里与是常数。

合并特解和与齐次方程解，可以得到通解：

选择坐标轴，让，代回

其中，是离心率。这是圆锥曲线的极坐标方程，坐标系的原点是圆锥曲线的焦点之一。假若，则所描述的是椭圆轨道，于是证明了开普勒第一定律。

开普勒第二定律

开普勒第二定律的内容

内容：连接行星和太阳的线段在相等时间间隔内扫过的面积相等2。

行星在椭圆轨道上的轨道半径和角速度会变化：当行星更接近太阳时，运行得更快；当远离太阳时，运行得更慢。值得注意的是，原本开普勒是通过一些仅近似正确或完全错误的假设，得出

来源: 百度百科

内容资源由项目单位提供