成像系统我们都不陌生，从摄像机到手机镜头，从天文望远镜到生物显微镜，光学透镜作为传统成像系统的核心元件，通过对光线的折射与对焦，实现了光学系统的成像功能，帮助我们看清宏观宇宙与微观世界。然而，传统透镜系统在应用中显现出一系列的限制和局限性。其中，成像质量受限是最为突出的问题之一，包括色差、畸变等，这些问题影响了图像的清晰度和准确性。为了提升成像质量，传统的方法通常是使用更复杂的透镜模组，这又使得系统的口径和重量增加，极大地影响了了光学系统的便携性，限制了其在许多场景中的应用。

色差

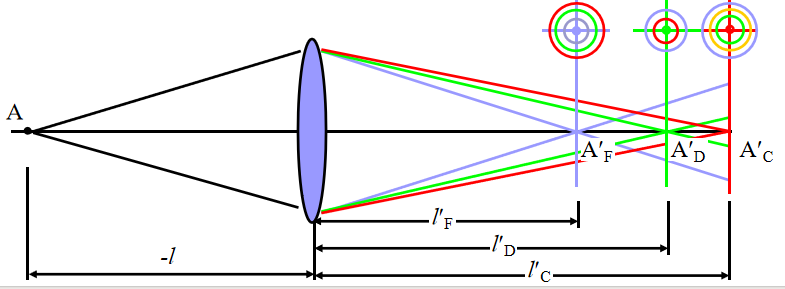
色差源于不同波长的光在透镜中折射率不同，导致各色光线在成像时无法聚焦在同一平面上。透镜会将红光、蓝光、绿光等不同颜色的光线聚焦在不同的点上，影响图像的精细度和色彩准确性。

畸变

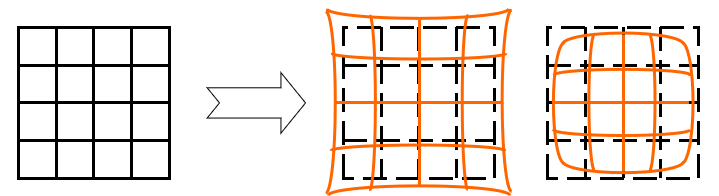
畸变表现为图像几何形状的扭曲或变形。当透镜不能保持物体形状的比例关系时，图像的边缘部分往往会出现拉伸或压缩现象。畸变一般分为两种类型：桶形畸变，图像边缘向外扩张，呈现出桶状；枕形畸变，图像边缘向内收缩，像枕头一样。

计算光学成像技术的发展突破了传统光学系统依赖复杂的透镜组这一局限，不再受限于光学系统的大小、形状和焦距等物理参数。其利用光学信号与算法的结合，通过算法来补偿光学系统的不足。其中，无透镜成像是计算光学的分支之一。顾名思义，无透镜系统的成像过程不需要透镜的参与，而是通过衍射光学元件对光线进行调制，再通过数学方法进行图像的重建。无需透镜，这种成像系统听起来晦涩而不可思议，但想要理清其背后的物理原理并不复杂，我们从简至繁逐一了解。

光的波动性、干涉与衍射

在理解无透镜成像之前，首先要了解光的特性。在成像过程中，光可以被看作是一种波，就像水波一样。当光遇到透镜时，透镜会通过改变光波的传播方向，将它们聚焦到一个点上，从而形成我们能够看到的清晰图像。这就是传统成像系统中的基本原理。

然而，当光遇到障碍物或经过狭小的缝隙时，就像水波遇到石头会绕过去一样，光波也会发生弯曲。这种“弯曲”现象在光学上被称为“衍射”。同时，当光波以不同的路径传播的过程中，如果它们满足了一定的条件便会相互作用相互叠加，在某些区域始终加强，在另一些区域则始终削弱，形成稳定的强弱分布的现象，这种现象便叫做“干涉”。虽然听起来复杂，但日常生活中也有类似的体验。比如当我们在一个池塘中扔两颗石子，水面上会产生涟漪。当这些涟漪相遇时，水波会形成复杂的波纹，这就是类似于光波干涉现象。

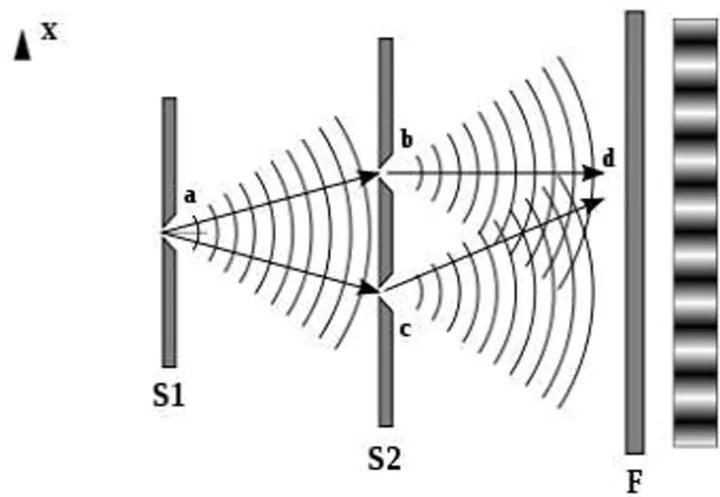
图双缝干涉

我们可以说，光学成像的本质是对光场信息的获取和解译。而光场信息便代表了光的种种内涵：光强、振幅、相位等物理信息。光强我们都很熟悉，光的相位相对难以理解，我们可以认为其代表了光波在一个周期内的位置，而这种周期位置中隐含着关键的空间结构信息。传统成像系统中，所记录的信息仅包含光强。利用先进的光学技术和计算方法，如果能够捕捉和记录这些光场的完整信息，我们就可以重建出比传统成像方式更加细致、精确的图像和信息。这正是新一代成像技术的核心思想，也是计算光学成像的重要思路。而菲涅尔波带片编码无透镜成像技术正是这一思想的典型代表。

菲涅尔孔径编码：光的再调制

菲涅尔波带片是一种基于菲涅尔衍射原理的特殊光学元件，它由一系列同心的透明和不透明区域组成，这些区域称为“波带”，并根据特定的半径规则交替排列。与传统光学透镜不同，菲涅尔波带片菲涅尔波带片的设计通过调节不同波带的尺寸和间距来控制光波的相位差，从而在空间中实现对光场的调制。

具体来说，当平行光束或点光源的光线照射到菲涅尔波带片上时，光波穿过透明的波带，而在不透明的波带部分被阻挡。但由于波带已经经过设计，所以每光线穿过不同波带时，传播的距离会有所不同。当光波传播的路径长短不同，光波的相位就会发生变化。例如，如果一条光线经过较长路径，它的波峰可能已经移动到了波谷的位置，表现为相位的偏移。当两条光线在成像点汇合时，它们可能已经走过了不同的距离。这就意味着，两条光线的波动状态可能已经不再同步了，从而产生了相位差。

这种相位差引发的干涉效应使得在成像平面上形成特定的光场分布，而这一光场分布包含了被调制的物体信息。菲涅尔孔径编码正是基于这一光场调制原理。通过波带片的设计和相位调制，菲涅尔波带片能够将物体的复杂光场信息编码成独特的干涉图案，而这些图案在传统成像系统中是无法直接获得的。由此可知，所谓编码，指的便是将数学变换在成像中的物理表现形式。不同于传统成像系统中“物点—像点”的简单一一对应关系，菲涅尔孔径编码打破了这种束缚，将成像过程的重点从物理透镜的光学成像转移到了光场信息的计算解码上。

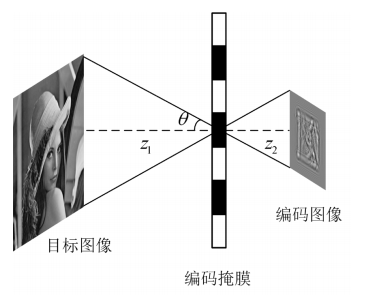
图编码示意图

从光场调制到图像重建：算法在无透镜成像中的角色

菲涅尔孔径编码解释了光场信息如何通过相位调制和干涉效应进行编码。然而，经过调制的光场信息并不能直接形成我们熟悉的图像。求解无透镜成像模型可以通过逆转编码过程，从传感器记录的编码图像中恢复原始的场景图像，以实现对目标的精确成像和重建。但是在无透镜成像中，传感器捕捉到的图像看上去可能是模糊、扭曲的。如何从这些复杂的“编码图像”中恢复出清晰、可识别的图像，就要依赖强大的计算算法。

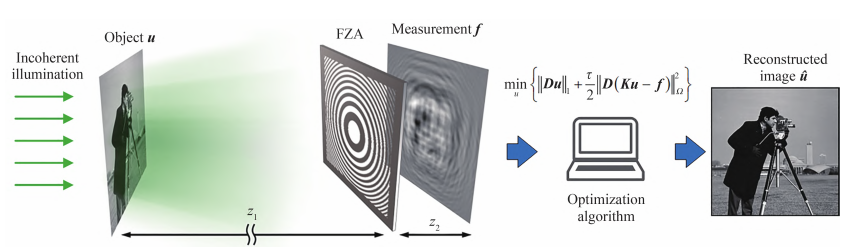
图编码成像示意图

压缩感知：用有限信息重建完整图像

无透镜成像系统的一个关键优势是能用较少的数据重建高质量的图像。这依赖于压缩感知算法。传统成像需要高分辨率传感器捕捉大量信息，而压缩感知能在有限采样下，通过数学模型重建出完整图像。它类似于拼图，即便只获得部分信息，算法也可以推导出整体，降低了对传感器分辨率的要求，并提高了成像灵活性。

傅里叶变换：解码光场中的频域信息

在无透镜成像中，傅里叶变换用来将图像从空间域转换到频率域。通过分析光场的频率信息，算法能够提取出光波中的振幅和相位信息，重建物体的结构与细节。傅里叶变换让算法像解码“光的密码”一样，从复杂的光干涉图案中还原出物体特征。

全变差正则化：提升图像质量

尽管无透镜成像可以重建图像，但可能会受噪声和伪影影响。全变差正则化算法帮助减少图像中的噪声，增强边缘清晰度。它能够保留重要的图像细节，抑制不必要的干扰，使最终的图像更加清晰、准确。

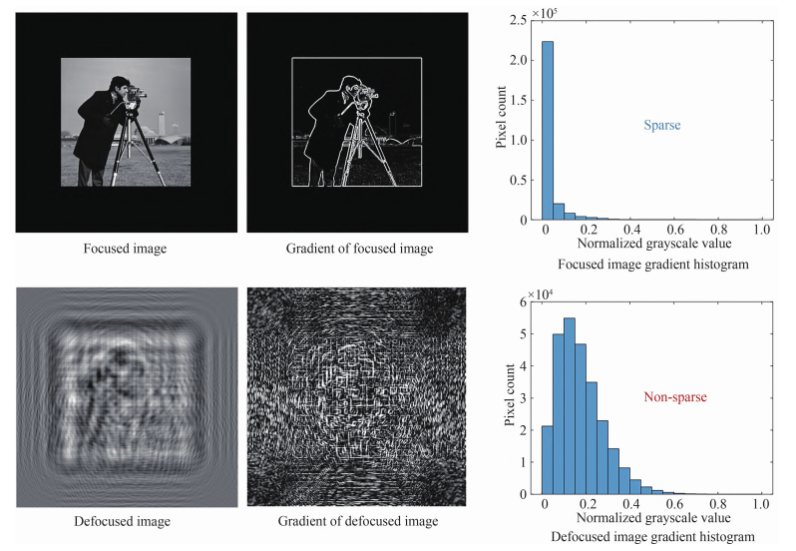
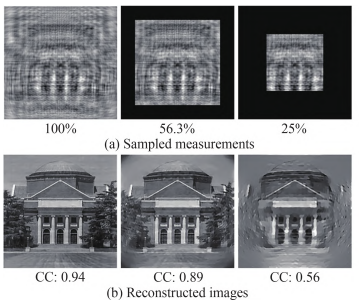
图算法处理与从重建结果示意图

传统的光学系统通过复杂的光学透镜设备实现了从物体到图像平面的点对点成像，但其几何性质的限制制约了其发展。而无透镜成像系统利用轻质平面编码装置替代透镜，有效地降低了成像系统的尺寸和成本。作为新兴的成像技术，势必会有广袤的发展空间。

参考文献

马辉辉.基于扩散模型的多相位菲涅耳孔径编码无透镜成像[D].南昌大学,2024.

吴佳琛,曹良才.基于压缩感知的菲涅尔孔径编码无透镜成像（特邀）[J].光子学报,2022,51(07):267-276.

策划制作

作者丨蔡文垂 中国科学院长春光学精密机械与物理研究所 研究生

审核丨胡志娟 上海师范大学数理学院物理系副教授

来源: 科普中国新媒体

内容资源由项目单位提供