在电磁学的发展中，矢势曾被认为是仅为数学方便而引入的矢量。直到1959年，Yakir Aharonov和David Bohm提出可以用实验的方法验证，在没有外部磁场的情况下，电子波函数的相位可以受到电磁势的影响，即AB效应。这意味着矢势是一种物理实在。最终实验得以证明，也彻底改变了人们对于这一量子效应的认识，相关应用得以长足发展。而这一效应背后反映了更深刻的物理与数学。

撰文 | 董唯元

在20世纪众多伟大的物理学发现中，AB效应（Aharonov–Bohm effect）的验证具有里程碑意义。简单来说，这是一种量子效应，指电磁矢势可以改变电子的量子相位。尽管早期其他物理学家对其也有提及，但直到物理学家Yakir Aharonov和他的博士导师David Bohm在1959年再次独立提出[1]，并于次年实验证实[2]，这一效应才得到大家的关注和重视。

对物理学家来说，证实这一效应的意义有点像考古学家挖到了孙悟空的墓，它使一个大家原以为是人为构造的虚幻对象，在客观世界中彰显出了真实存在的迹象。

考古学家在福建挖掘的那个孙悟空墓，里面当然没有孙悟空的遗骸，那只是人们为了行祭奠之礼而建的“形祭冢”。而AB效应则是实打实地表现了电磁理论中“矢量势”这个抽象对象的真实“遗骸”——双缝干涉条纹的漂移。这个效应引发了后续一系列深刻且重要的认知升级，并以出人意料的方式联系着许多理论领域。

在介绍AB效应具体内容之前，让我们先稍微储备一些相关基本概念。

Yakir Aharonov（1932-；左）与David Bohm（1917-1992）

用电势描述静电场

中学物理课本里，电磁场用E和B这两个矢量场来描述，E是电场强度，B是磁感应强度。这是沿承着法拉第场线观念，对电磁场最朴素直接的刻画。另外，在描述静电场时，还可以使用电势（也称电位）φ这个标量场，代替E进行完全等价的刻画。

E和φ的关系，用稍微超出高中知识的数学语言来讲，就是E=-∇φ。这里的符号“∇”是对空间求导的意思，“∇φ”叫作φ的梯度。如果把φ比喻成空间各处的温度，那么E的方向就是躲避高温寻求凉爽的最佳出逃方向，而E的大小则由出逃方向上的温差决定。

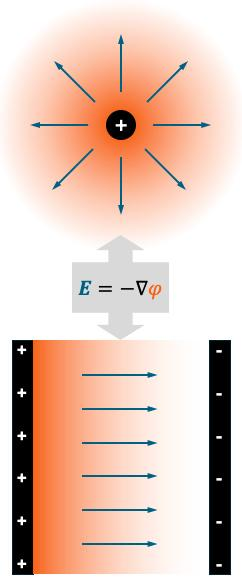
用E或φ两种方式所描述的静电场是完全等价的，鉴于φ是标量，E是矢量，显然用φ来进行推演和计算要方便很多。使用φ还有其他的好处，比如用φ描述的静电场天然保证场线不会绕成闭合环路，而在用E描述时，这一点则属于需要额外单独列出来的限制条件。

如此看来，似乎φ比E更基本，抽象程度也更高——E是由φ导致的结果。不过，在空间中摆放好一些电荷之后，空间每点处E的取值就完全确定了，可是φ的取值却并不确定。事实上，如果把所有点的φ值都同时加上个相同的值，那么整个空间中φ的分布起伏完全没有变化，就像把一座山整体抬升，完全不影响山峦形状一样。

那么到底该如何看待电势φ这个量？它究竟是比电场强度E更基本的客观物理量，还是仅具有计算意义的数学抽象？

当然不管怎么判断，我们此刻至少知道了φ值的选取有相当大的自由。或者说空间某点处的φ值本身是多少根本不重要，真正重要的只是任意两点之间φ值之差，也就是电势差。这个电势差还有个我们耳熟能详的名字——电压。

描述磁场的矢量势

高中物理只介绍了静电场的两种等价描述，没有将这种方式延伸到磁场。大学的电磁学课本里，还会再出现一个类似电势φ的物理量，叫作矢量势或矢势，用字母A表示。如同φ和E能等价地描述静电场一样，矢势A和磁场强度B能等价地描述磁场。

与φ略有不同的是，A是一个矢量场，由A得出B的方式也不是求梯度，而是求旋度，B=∇×A。这个符号与叉乘的含义解释起来，倒也不难：其实就是把A视为一大锅水，如果某处存在漩涡，那么漩涡中心被裹挟着原地自转的那些水分子，沿自转轴方向排列成的线，就是该处的磁场B的场线。

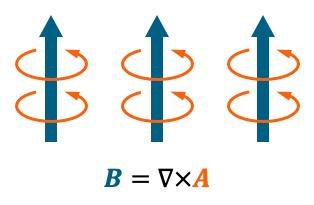
如果盛水的锅足够大，在无穷远的边界处所有水都是静止的，漩涡都被限制在有限的空间里折腾，那么可以想象，这些漩涡所对应的磁场线必然全都是闭合线。这就显示出用矢势A描述磁场的一个好处，它不需要额外补充声明，天然就能保证所有磁场线都闭合这一事实。

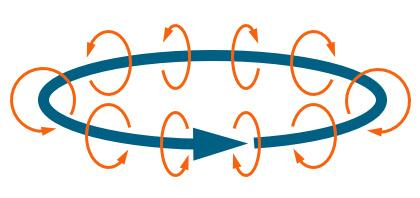
磁场线如果出现断头的端点，这个端点在物理意义上就是一个磁单极子。每根磁场线都闭合这件事，其实就意味着世界上不存在磁单极子。而借助矢势A来理解，不仅一切变得顺理成章，我们还能更深刻地意识到，磁单极子的出现竟然会破坏宇宙的全局对称性，使宇宙这一大锅水整体上出现了漩涡。

在有些文献中A也被称为磁势，但使用这个名字的人并不太多。因为在动态的电磁场中，变化着的A会对电场强度E也产生贡献。事实上变化着的电磁场中， E和B已然是个不可分割的统一体，自然相对应的φ和A也没必要非得分开看待。

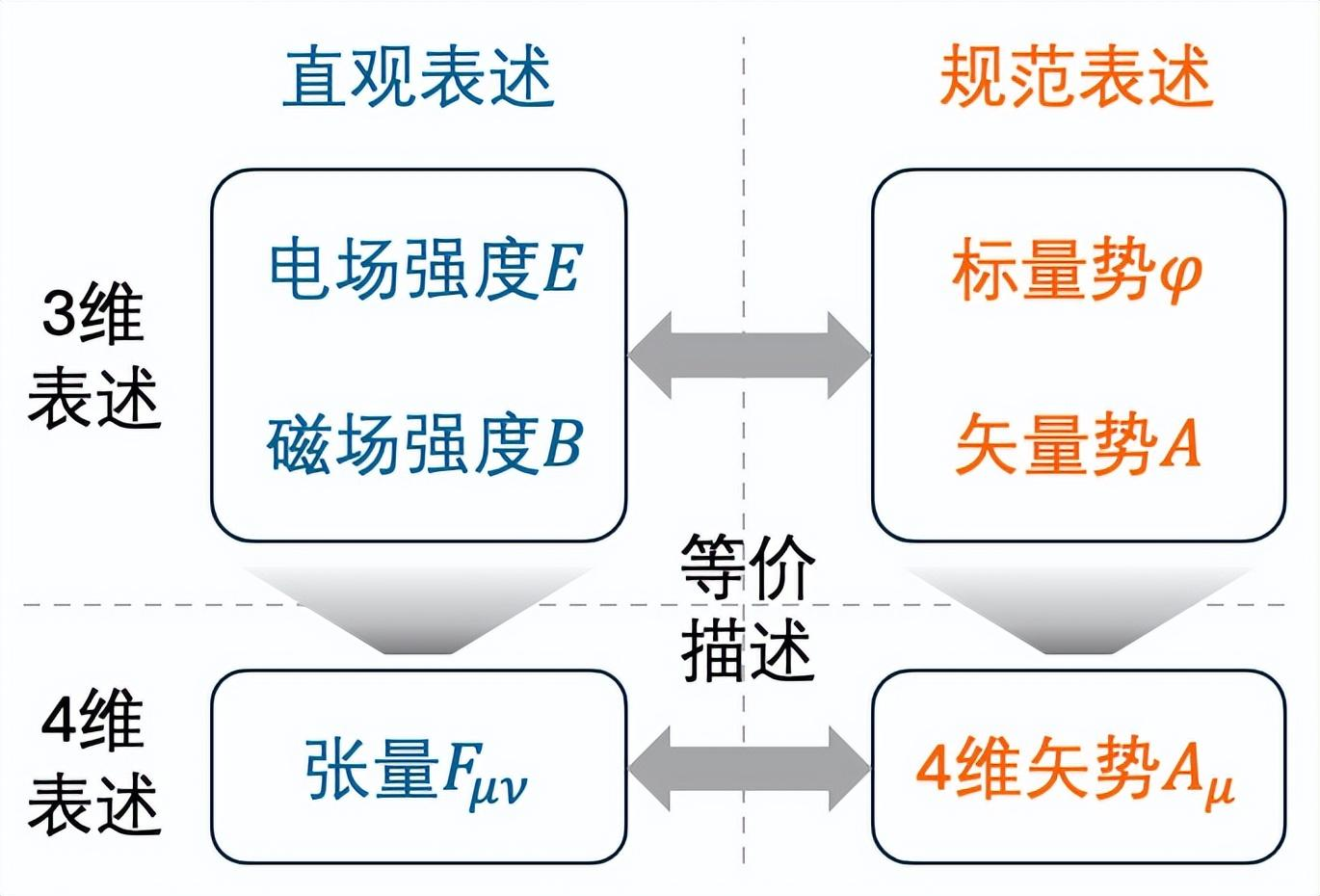
在上图中，右半边的表述方式被称为规范表述，此处的“规范”（gauge）是个特定物理概念，并不是整洁漂亮的意思（编者注：可参见曹则贤《物理学咬文嚼字之五十八 Norm and Gauge》）。至于它到底代表什么含义，还得请读者耐心听我娓娓道来。

规范自由

前面已经提到，在用φ刻画静电场时，可以相当任性地为φ取值。而所谓“规范”，大致含义就是φ取的某个具体的值。这种特点在矢势A身上也有体现，而且还更加任性。我们可以在某个A上再随意叠加个矢量场，因为A中的漩涡才对应着磁场B，如果叠加的矢量场中没有漩涡，那么叠加前后两个不同的矢势A和A'，所描述的磁场B却完全相同。

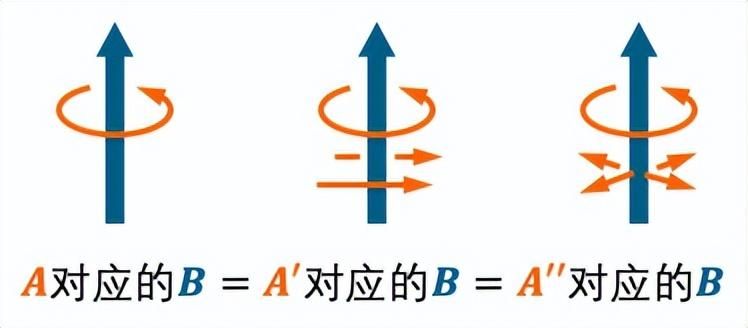
至于可随意增删的那部分矢量场，不仅姿态样貌任选，还可以不断变化，只要不出现新的漩涡即可。上图中的A、A'、A''就是同一个磁场B所对应的3个不同的规范。显然同一个电磁场的E和B可以对应着无数个规范，具体计算时只需要从中挑选一个最便于计算的取值即可。

φ和A所拥有的这种自由取值的特性，就叫作规范自由。如果某个场的描述方式具备规范自由，那么这个场就被归类为规范场。电磁场能用φ和A书写，所以电磁场就是一种规范场。

事实上在现代物理学中，所有传递相互作用力的场，统统都是规范场。同时现代物理学观念将粒子视为某种场吞吐能量的最小单元，所以那些规范场的最小能量单元就是各种作用力的承载者。光子是电磁场的最小能量单元，承载电磁作用；胶子是胶子场的最小能量单元，承载强相互作用；W和Z则是承载弱作用的基本能量单元。

在一些旧课本里，规范自由这个词会被说成“规范自由度”，这多出来的一个“度”字，曾使许多初学者产生困惑和误解。虽然可自由取值这一特点使φ和A看起来颇有些像电磁场拥有的某种自由度，但是当取值在不同规范之间变换时，电磁场本身其实是纹丝不动的，这就跟真正自由度的概念不相容了。

因为“规范自由度”不能容纳运动，这个所谓的自由度也就与能量变化无关，所以它并不是个正统意义上的自由度，我们还是称其为规范自由比较合适。不过“变换之后一切都没变”这句描述，似乎又提醒着我们什么。

是的，这不就是对称性嘛！规范自由其实是一种对称性的体现。而这种称性跟圆盘子转动起来的那种整体对称的味道还不一样，规范对称性是空间中每点私有的对称性，灵活性要大得多。

回想一下我们对矢势A做出的规范变换，新叠加的矢量场在空间每点不一定相同，不同点的变换步调也不需要整齐划一，只要新叠加的场是个光滑连续且不带来新漩涡的场，就都能使磁场保持不变。

为了区别，像圆盘子整体转动之后保持不变的那种对称性被称为“全局对称性”，而规范对称性则属于“局域对称性”。后者是蕴含丰富内容的理论宝藏，自20世纪中叶之后，更是成了推动理论物理研究快速进展的核动力发动机。

开启新世界之门的理论钥匙，当属杨振宁和米尔斯提出的杨-米尔斯理论，而实验方面最重要的标志性里程碑，则无疑是AB效应。

AB效应实验内容

在AB效应被提出之前，物理学家们已经认识到φ和A所代表的规范对称性。但是大多数物理学家仍然认为它们本身不会造成任何可观测的现象，所以无关乎真实世界的客观状态，纯粹只是数学上的奇技淫巧。因此这种对称性也只是人为构造的虚幻之物，自然没什么兴趣挖掘。AB效应的实验验证彻底改变了这一观念。

实验的具体内容其实非常简单，就是在双缝干涉实验装置中增加了一个螺线管，当螺线管中有电流通过时，接收屏上的干涉条纹会发生一定距离的偏移。我们知道通电螺线管能产生磁场，由于螺线管的约束作用，磁场B只分布在螺线管内部，就是下图中的蓝色区域内B≠0，而在螺线管之外B=0。

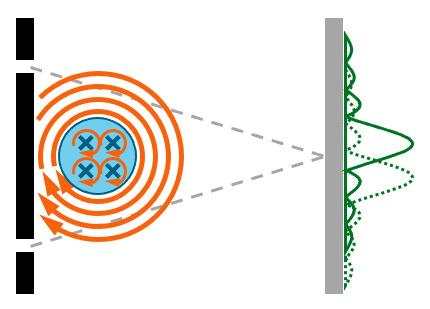
但是，螺线管外的矢势A却不为零。按照磁场B与矢势A在数学上的关系，B=∇×A，这个关系的积分形式是说，空间中任意一个闭合环路上A的积分，就等于这个环路所圈起来的面上的总磁通量。既然中间存在非零的磁通量，那么外围任意闭合环路上的A就不可能处处为零。

我们可以把A场中的每点想象成一名舞蹈演员，实验设定下螺线管内，也就是蓝色区域，所有演员都在原地自转，外围的演员则是在绕着螺线管转圈。

而运动电荷在磁场中会受力这件事，可以想象成电荷都是有特别偏爱的小伙，只对原地自转的姑娘着迷，遇到自转的舞蹈演员就会偏转前进的方向，而对那些没有自转的演员就完全无感，仍然保持原来的方向行走。

螺线管所摆放的位置，恰好使通过双缝的电子途径B=0且A≠0的区域到达接收屏。按说电子在经过这些区域的时候，行走方向不会发生变化，然而接受屏上的干涉条纹居然发生了移动。由此可见，造成干涉条纹变动的原因肯定不是磁场B，必然是矢势A。这即是AB效应。

AB效应的意义首先就是证明了矢势A确实是客观物理对象，即使在不产生磁场的时候，也能彰显出它对这个世界的影响，产生可观测物理现象。其次，这一效应暗示，当电子路过电磁场时，E和B所能影响的只是电子呆板木讷的外在行为表现，φ和A才更能触及电子闷骚躁动的内心世界。

可是，φ和A当初明明就是作为E和B的等价表述被引入的，数学形式上的等价性看起来严丝合缝，这两套表述究竟在什么情况下会产生差异呢？答案就是相位，确切地说，是量子相位。

量子相位

描述电磁场时，用E和B写出的麦克斯韦方程组有4个方程，改用φ和A书写则会变成2个方

描述的电磁场始终是同一个物理对象，对带电小球在电磁场中的运动都会给出相同的预测。

如果依照经典物理图像，把电子看做带电荷的小球，那么电子在经过B=0且A≠0的区域时就不会感受到电磁场的作用，运动状态也就不会发生任何改变。可是在量子理论中万物都是波，电子自然也不例外，不能再被看作小球。我们暂时姑且将电子想象成振动着前行的一小团波包。

当电子经过螺线管旁边时，由于B=0，这团波包表面看起来仍然目不斜视地笔直向前，然而此时矢势A却已然偷偷地改变了电子的相位。原来电子这位小伙的眼里并不只有那些原地自转的姑娘，即使遇到不自转的姑娘时内心也会有波澜，只不过脚下行走的路线没有体现出来罢了。

读者尽可以借助这个比喻来感受矢势A对电子的相位施加的影响，不过为了减少可能造成的误解，这里还得澄清一下：所谓的电子振动并不是电子得了帕金森症，在3维空间里颤颤巍巍地行走，而是电子自身量子态随时间和空间位置的变化。

了解复数运算的朋友立即就会发现，这种波动性恐怕跟测量结果没什么关系。因为对任意的复数z和实数θ，总有|z|=|ze^iθ|，也就是说，无论新增加的那些相位参数怎么变化，测量到活猫死猫的概率都没有变化。

正因为量子相位对测量结果而言似乎刷不出存在感，只能在自己与自己干涉的时候才得以显现，所以在相当长一段时间里，物理学家们普遍认为相位本身是一个不可观测量。显然，AB效应的发现，结结实实地否定了这种观点。电子的相位就在矢势A的影响下发生了变动，而且这种变动还形成了可观测结果。

AB效应与几何相位

双缝干涉中一个电子裂成两个“影子分身”，这两个分身分别经过了两条狭缝并在接收屏处汇合。本着“为了图方便随意使用数学语言”的精神，可以把接收屏处电子的量子态写成

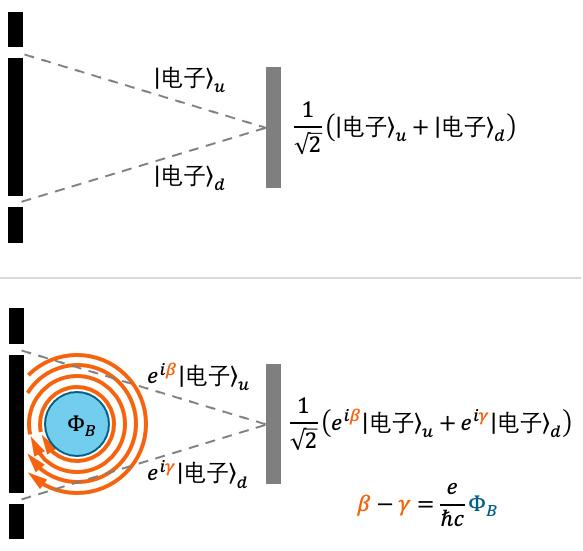
基本常数，只有磁通量才是与条纹移动相关的唯一变量。也就是说，尽管从缝到屏直线行走不会经过任何磁场，但屏处的电子状态里，包含了磁通量的信息。

这个关系很有趣，值得咀嚼感受。如果某人不愿意接受矢势A的客观真实性，只认定磁场B才是物理真实的，那么他其实可以从这个关系中获得一丝丝支持。

比如可以宣称，电子的两个分身在离开狭缝后并不是各自闷头奔跑，而是以某种神秘的方式隔空拉起手，摸索了两条路径之间的整片区域，并最终携带着搜集到的所有信息来到接收屏。

在这个理论图像里，就不需要承认矢势A的真实性，仍然可以解释AB效应。不过代价是要解释那个更令人难以接受的隔空拉手机制，恐怕还不如干脆承认A的物理真实性算了。

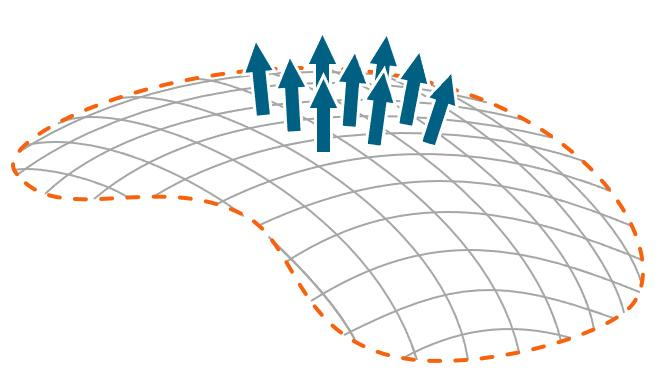
除了用来复活旧观念，前面那个相位与磁通量的关系，还隐约体现出空间整体拓扑结构对量子相位可以造成可见影响。不过在AB效应提出的当时，物理学家们并没有立即意识到这一点，直到1984年数学家和物理学家Michael Berry提出了几何相位的概念**[4]**，人们才能够直观地体会到AB效应几乎就是几何相位的一种具体实现。

几何相位的大意是指，量子态在空间中绕闭合路线旅行一周回到出发点时，如果空间的拓扑结构比较特殊，那么在量子相位中就会显现出相应的变化。这样空间整体拓扑性质，神奇地与量子相位建立起了联系。

对比几何相位的图像，AB效应中电子分别经过两条路径最终到达同一点，在此处的相位体现出了两条路径所包围的空间中的电磁场。稍微画个示意图，就能体会到这两者的相似度是如此的一目了然。

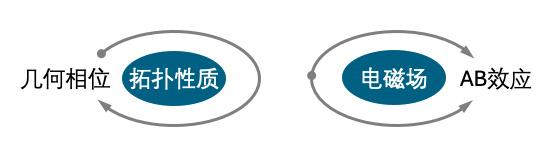
几何相位概念的提出，使我们拥有了一个新的视角重新解读AB效应：由于电磁场的存在，电子眼中的空间发生了某种拓扑结构的变化，于是就产生了相位差。怎么样？是不是“玄幻色彩”又增加了些？

1998年的沃尔夫奖同时授予了Yakir Aharonov和Michael Berry，以表彰AB效应和几何相位这两项重要理论发现。这不仅反映出AB效应和几何相位之间紧密的联系，同时也体现出这两项理论对现代物理学的许多领域都有相当重要的价值。

参考文献

[1] Aharonov, Y; Bohm, D (1959). "Significance of electromagnetic potentials in quantum theory". Physical Review. 115 (3): 485–491. Bibcode:1959 PhRv..115..485A. doi:10.1103/PhysRev.115.485.

[2] Chambers, R.G. (1960). "Shift of an Electron Interference Pattern by Enclosed Magnetic Flux". Physical Review Letters. 5 (1): 3–5. Bibcode:1960 PhRvL...5....3C. doi:10.1103/PhysRevLett.5.3.

[3] Aharonov, Y; Dohrlich, D (2005). “Quantum Paradoxes: Quantum Theory for the Perplexed”.

[4] M. V. Berry (1984). "Quantal Phase Factors Accompanying Adiabatic Changes". Proceedings of the Royal Society A. 392 (1802): 45–57. Bibcode:1984RSPSA.392...45B. doi:10.1098/rspa.1984.0023. S2CID 46623507

特 别 提 示

1. 进入『返朴』微信公众号底部菜单“精品专栏“，可查阅不同主题系列科普文章。

2. 『返朴』提供按月检索文章功能。关注公众号，回复四位数组成的年份+月份，如“1903”，可获取2019年3月的文章索引，以此类推。

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。

来源: 返朴

内容资源由项目单位提供