定义

直线方程一般有以下八种描述方式：点斜式，斜截式，两点式，截距式，一般式，法线式，法向式，点向式。

过原点向直线做一条的垂线段，该垂线段所在直线的倾斜角为α，p是该线段的长度。则该直线方程的法线式为：xcosα+ysinα-p=0。其中p为原点到直线的距离，θ为法线与X轴正方向的夹角。

推导方法

斜截式推导

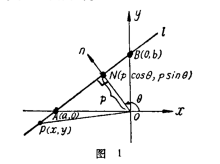设坐标平面内的任意一条直线l在y 轴上的截距为b，法线n交直线l于点N， ，x轴的正方向到法线n的正方向的角为θ，则直线l和y轴的交点B的坐标与点N的坐标分别为（0，b）与（pcosθ，psinθ）（图一）

由 得

故

解得

又由法线n的斜率 知

直线l的斜率

将这里的K和b的值代入直线方程的斜截式得

若 ，方程两端都乘以 后，将各项都移至等号左边得

若 ，仍有

两点式推导

因直线l经过点N（pcosθ，psinθ）及点B （图一），故

因此

两边都乘以 后，展开得

将两项都移至等号左边得：

因为 ，所以直线l不与x轴平行，因而法线n不与x轴垂直，于是

所以

截矩式推导

设直线l在x轴上的截距为a（图一），用与求 类似的方法可求得

将这里的a和b的值代入直线方程的截距式得

整理得

勾股定理推导

设P（x，y）为直线上的任意一点（ 下文中的p皆与此意义同），则图一中：

故

两边平方并整理得

来源: 百度百科

内容资源由项目单位提供