内容

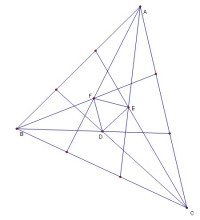将三角形的三个内角三等分，靠近某边的两条角三分线相交得到一个交点，则这样的三个交点可以构成一个正三角形。

证明方法

该定理以其美妙和证明困难著称，到目前为止，已经有很多证明方法。

证法一

设△ABC中，AF、 AE、BF、BD、CD、CE为各角的三等分线，三边长为a,b,c,三内角为3α，3β，3γ，则α+β+γ=60°。

在△ABF中，由正弦定理，得AF=csinβ/sin(α+β)。

不失一般性，△ABC外接圆直径为1，则由正弦定理，知c=sin3γ，所以AF=

（sin3γ*sinβ）/sin(60°-γ)=[sinβ*sinγ(3-4sin²γ)]/[1/2(√3cosγ-sinγ)]=

2sinβsinγ（√3cosγ+sinγ）=4sinβsinγsin（60°+γ）.

同理,AE=4sinβsinγsin(60°+β)

∴AF:AE=[4sinβsinγsin(60°+γ)]：[4sinβsinγsin(60°+β)]=sin(60°+γ):sin(60°+β)=sin∠AEF:sin∠AFE

∴∠AEF=60°+γ,∠AFE=60°+β.同理得，CED=60°+α

FED=180°-CED-(AEF-α-γ)=180°-60°-α-60°+α=60

∴△FED为正三角形。1

证法二

∵AE：AC=sinγ：sin（α+γ），

AF：AB=sinβ：sin（α+β） ，

AB：AC=sin3γ：sin3β，

∴AE:AF=（ACsinγ/sin（α+γ））：（ABsinβ/sin（α+β）），

而sin3γ：sin3β=（sinγsin(60°+γ)sin(60°-γ) ）：（sinβ sin(60°+β) sin(60°-β) ），

sin（α+β）sin(60°-β)=sin（α+γ）sin(60°-γ)，

∴AE：AF=sin(60°+β)：sin(60°+γ)，

∴在△AEF中，∠AEF=60°+γ，

同理∠CED=60°+α，

∴∠DEF=60°，

同理∠DFE=60°，

∴△DEF为正三角形。

来源: 百度百科

内容资源由项目单位提供