两角和（差）公式

正弦公式

余弦公式

正切公式

以上三式被称为两角和（差）的三角函数公式。1

公式证明

如图1，为半径为1的单位圆。

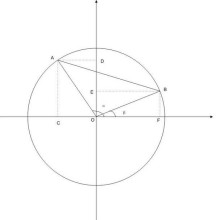
根据余弦定理：

既

根据勾股定理：

故

又

且

化简后，即

联立（1）（2），知

此即两角差的余弦公式。

根据诱导公式可知：

此即两角差的正弦公式。

将前两式相除，即得对应的正切公式。

证毕。1

历史

两千多年前亚历山大的数学家希帕霍斯 (Hipparchus，180B.C．~125B.C．)利用相当于三角函数和差角公式的结果制作了目前所知的第 一个弦表，可惜未能流传下来，后来托勒密也利用相当于和差角公式，制成现存最早的三角函数的弦表，弦表在后来的天体测量与大地测量中有 着非常重要的应用。 一千七百多年前，亚历山大的数学家帕普斯给出了正弦函数和角公式的几何模型。2

来源: 百度百科

内容资源由项目单位提供