定义

一般地，自变量x和因变量y之间存在如下关系：

一般式：y=ax2+bx+c(a≠0，a 、b、c为常数)，则称y为x的二次函数。

顶点式：y=a(x-h)2+k(a≠0，a、h、k为常数)

交点式（与x轴）：y=a(x-x1)(x-x2)(a≠0，x1、x2为常数)

重要知识：a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下2。IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大。

二次函数表达式的右边通常为二次。

x是自变量，y是x的二次函数

一元二次方程求根公式

当b2-4ac>0 时

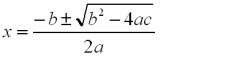
当b2-4ac=0时

x1=x2=-b/2a

表达式

①一般式

y=ax2***+bx+c***(a,b,c为常数,a≠0)

②顶点式

[抛物线的顶点 P(h，k) ]：y=a(x-h)2+k(a,h,k为常数,a≠0)

③交点式

[仅限于与x轴有交点 A(x1,0) 和 B(x2,0) 的抛物线]：y=(x-x1***)(x-x2)***(x1,x2为常数,)3

转化

3种形式的转化∶

①一般式和顶点式

对于二次函数y=ax2+bx+c，其顶点坐标为*(-b/2a,(4ac-b2)/4a)*，即

h=-b/2a=(x1***+x2)/2***

k=(4ac-b2***)/4a***

②一般式和交点式

x1,x2=[-b±√(b2-4ac)]/2a(即一元二次方程求根公式)4

有关性质

抛物线的性质

1.抛物线是轴对称图形。对称轴为直线x = -b/2a。

对称轴与抛物线唯一的交点为抛物线的顶点P。

特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）

2.抛物线有一个顶点P，坐标为P ( -b/2a ，(4ac-b2)/4a )

当-b/2a=0，〔即b=0〕时，P在y轴上；当Δ= b2-4ac=0时，P在x轴上。

3.二次项系数a决定抛物线的开口方向和大小。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

|a|越大，则抛物线的开口越小。

4.一次项系数b和二次项系数a共同决定对称轴的位置。

当a与b同号时（即ab>0），对称轴在y轴左；

当a与b异号时（即ab<0），对称轴在y轴右。

5.常数项c决定抛物线与y轴交点。

抛物线与y轴交于（0，c）

6.抛物线与x轴交点个数

Δ= b2-4ac>0时，抛物线与x轴有2个交点。

Δ= b2-4ac=0时，抛物线与x轴有1个交点。

Δ= b2-4ac<0时，抛物线与x轴没有交点。X的取值是虚数（x= -b±√b2－4ac乘上虚数i，整个式子除以2a）

当a>0时，函数在x= -b/2a处取得最小值f(-b/2a)=〔4ac-b2〕/4a；在{x|x<-b/2a}上是减函数，在{x|x>-b/2a}上是增函数；抛物线的开口向上；函数的值域是{y|y≥4ac-b2/4a}相反不变

当b=0时，抛物线的对称轴是y轴，这时，函数是偶函数，解析式变形为y=ax2+c(a≠0)

**7.**定义域：R

值域：（对应解析式，且只讨论a大于0的情况，a小于0的情况请读者自行推断）①[(4ac-b2)/4a，正无穷）；②[k，正无穷）

奇偶性：非奇非偶 （当且仅当b=0时，函数解析式为f（x）=ax2+c, 此时为偶函数）

周期性：无

解析式：

①y=ax2+bx+c[一般式]

⑴a≠0，a、b、c为常数。

⑵a>0，则抛物线开口朝上；a<0，则抛物线开口朝下；

⑶极值点：（-b/2a，(4ac-b2)/4a）；

⑷Δ=b2-4ac,

Δ>0，图象与x轴交于两点：

（[-b+√Δ]/2a，0）和（[-b-√Δ]/2a，0）；

Δ=0，图象与x轴交于一点：

（-b/2a，0）；

Δ<0，图象与x轴无交点；

②y=a(x-h)2+k[配方式]

此时，对应极值点为（h，k），其中h=-b/2a，k=(4ac-b2)/4a。5

二次函数的性质

特别地，二次函数（以下称函数）y=ax2+bx+c(a≠0)，

当y=0时，二次函数为关于x的一元二次方程（以下称方程），

即ax2+bx+c=0(a≠0)

此时，函数图像与x轴有无交点即方程有无实数根。

函数与x轴交点的横坐标即为方程的根。

1．二次函数y=ax2，y=ax2+k,y=a(x-h)2，y=a(x-h)2+k，y=ax2+bx+c(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

|| ||

当h>0时，y=a(x-h)**2的图象可由抛物线y=ax^2向右平行移动h个单位得到，

当h<0时，则向左平行移动|h|个单位得到．

当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；

当h>0,k<0时，将抛物线y=ax**2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；

当h<0,k>0时，将抛物线向左平行移动*|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k*的图象；

当h<0,k<0时，将抛物线向左平行移动*|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k*的图象；

因此，研究抛物线 *y=ax2+bx+c(a≠0)*的图象，通过配方，将一般式化为y=a(x-h)2+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．

2．抛物线y=ax2+bx+c(a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是(-b/2a，[4ac-b2]/4a)．

3．抛物线y=ax2+bx+c(a≠0)，若a>0，当x ≤ -b/2a时，y随x的增大而减小；当x ≥ -b/2a时，y随x的增大而增大．若a<0，当x ≤ -b/2a时，y随x的增大而增大；当x ≥ -b/2a时，y随x的增大而减小．

4．抛物线y=ax2+bx+c*(a≠0)*的图象与坐标轴的交点：

(1)图象与y轴一定相交，交点坐标为(0，c)；

(2)当△=b2-4ac>0，图象与x轴交于两点A(x1，0)和B(x2，0)，其中的x1,x2是一元二次方程ax2+bx+c=0

(a≠0)的两根．这两点间的距离AB=|x2-x1| 另外，抛物线上任何一对对称点的距离可以由2x|A+b/2a|（A为其中一点的横坐标）

当△=0．图象与x轴只有一个交点；

当△<0．图象与x轴没有交点．当a>0时，图象落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图象落在x轴的下方，x为任何实数时，都有y<0．

5．抛物线y=ax2+bx+c的最值（也就是极值）：如果a>0(a<0)，则当x= -b/2a时，y最小(大)值=(4ac-b2)/4a．

顶点的横坐标，是取得极值时的自变量值，顶点的纵坐标，是极值的取值．

6．用待定系数法求二次函数的解析式

(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式为一般形式：

y=ax2+bx+c(a≠0)．

(2)当题给条件为已知图象的顶点坐标或对称轴时，可设解析式为顶点式：y=a(x-h)2+k(a≠0)．

(3)当题给条件为已知图象与x轴的两个交点坐标时，可设解析式为两根式：y=a(x-x1)(x-x2)(a≠0)．

7．二次函数知识很容易与其它知识综合应用，而形成较为复杂的综合题目。因此，以二次函数知识为主的综合性题目是中高考的热点考题，往往以大题形式出现。

来源: 百度百科

内容资源由项目单位提供