基本介绍

1.用三角形的边和角来表示它的外接圆的半径

设在 中，已知一边和它的对角，那么用已知边和角来表示它的外接圆的半径R的公式是

很明显，这几个公式可以从正弦定理的推论导出。

2．用三角形的三边来表示它的外接圆的半径

设在 中，已知三边 ，那么，用已知边表示三角形的外接圆半径R的公式为：

其中 。

**证明：**因为

而

就是

所以(由海伦公式)：

3.用三角形的三边和面积表示外接圆半径的公式

公式中 是这三角形的三条边，S为三角形的面积。

内切圆半径

1．用三角形的三边来表示它的内切圆的半径

设在中，已知三边，那么，用已知边表示内切圆半径r的公式是

2．用三角形的边和角来表示它的内切圆的半径

设在中，已知三边和一角，那么，用已知边和角表示内切圆半径r的公式是

很明显，这个公式可以从半角定理导出。

相互关系

与三角形三边的关系

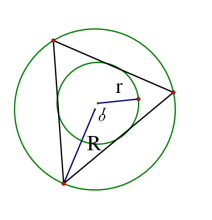
外接圆半径： ；

内切圆半径： ，

所以，同个三角形内外接圆半径定量关系：1

即

外接圆半径与内切圆半径

若r、R分别是△ABC的内切圆和外接圆半径，则二者满足以下关系：

**证明:**由内切圆、外接圆的半径公式中消去S得

利用正弦定理，把边长化为角度得

左边利用二倍角公式，右边利用三角形三角函数特殊关系化简得

整理得

△ABC的内切圆、外接圆半径分别为 r，R，大家知道有著名的 Euler公式：R ≥ 2 r。2

来源: 百度百科

内容资源由项目单位提供