定义

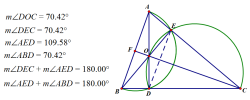
垂心是从三角形的各个顶点向其对边所作的三条垂线的交点。

锐角三角形垂心在三角形内部。

直角三角形垂心在三角形直角顶点。

钝角三角形垂心在三角形外部。

三角形三个顶点，三个垂足，垂心这7个点可以得到6组四点共圆。

口诀

三角形上作三高，三高必于垂心交。

高线分割三角形，出现直角三对整，

直角三角有十二，构成九对相似形，

四点共圆图中有，细心分析可找清。

性质

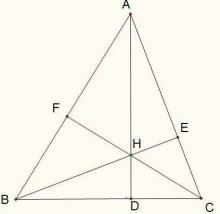设△ABC的三条高为AD、BE、CF，其中D、E、F为垂足，垂心为H，角A、B、C的对边分别为a、b、c，p=(a+b+c)/2．

1、锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外**.**

2、三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；

3、 垂心H关于三边的对称点，均在△ABC的外接圆上。

4、 △ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AH**·HD=BH·HE=CH·**HF。

5、 H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。

6、 △ABC，△ABH，△BCH，△ACH的外接圆是等圆。

7、 在非直角三角形中，过H的直线交AB、AC所在直线分别于P、Q，则 AB/AP**·tanB+AC/AQ·**tanC=tanA+tanB+tanC。

8、 设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。

9、 锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。

10、 锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短（施瓦尔兹三角形，最早在古希腊时期由海伦发现）。

11、西姆松定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。

12、 设锐角△ABC内有一点P，那么P是垂心的充分必要条件是PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA。

13、设H为非直角三角形的垂心，且D、E、F分别为H在BC，CA，AB上的射影，H1，H2，H3分别为△AEF，△BDF，△CDE的垂心，则△DEF≌△H1H2H3。

14、三角形垂心H的垂足三角形的三边，分别平行于原三角形外接圆在各顶点的切线。

15、三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。（垂心伴随外接圆，必有平行四边形）。

推论（垂心余弦定理）：锐角三角形ABC的垂心为H，则AH/cosA=BH/cosB=CH/cosC=2R（可引入有向距，推广到任意三角形）。

美国数学家 R ·A·约翰逊在其名著中，介绍 了三角形的一个美妙性质，即： 设AABC三条边BC、CA、AB的中点分别 为 D、E、F，则 AABC的外心是ADEF的垂心。3

16、等边三角形的重心把三角形的高分成2:1两段，靠近顶点的那段长度为高的三分之二。(高中学习中常用知识）

证明

证明：

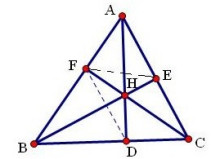如图1：

作BE⊥AC于点E,CF⊥AB于点F,且BE交CF于点H,连接AH并延长交BC于点D。只要证明AD⊥BC即可。

因为CF⊥AB,BE⊥AC

所以 四边形BFEC为圆内接四边形.

四边形AFHE为圆内接四边形.

所以∠FAH=∠FEH=∠FEB=∠FCB

由∠FAH=∠FCB得

四边形AFDC为圆内接四边形

所以∠AFC=∠ADC=90°

即AD⊥BC.

向量

具备条件

设点H为锐角三角形ABC的垂心，向量OH=h，向量OA=a，向量OB=b，向量OC=c，

则

垂心坐标的解析解：

设三个顶点的坐标分别为(a1，b1)、(a2，b2)、(a3，b3)，那么垂心坐标 ， 。

其中，

垂心的向量特征：三角形ABC内一点O，向量OA·OB=OB·OC=OC·OA，则点O是三角形的垂心

证明

由OA·OB=OB·OC，得

OA·OB-OC·OB=0

∴(OA-OC)·OB=0

∴CA·OB=0，即OB垂直于AC边

同理由OB·OC=OC·OA，可得OC垂直于AB边

由OA·OB=OC·OA，得OA垂直于BC边

∴点O是三角形的垂心。

来源: 百度百科

内容资源由项目单位提供