定义

周期

在非常小的振幅（角度）下，单摆做简谐运动的周期跟摆长的平方根成正比，跟重力加速度的平方根成反比，跟振幅、摆球的质量无关。

公式

单摆是一种理想的物理模型，它由理想化的摆球和摆线组成．摆线由质量不计、不可伸缩的细线提供；摆球密度较大，而且球的半径比摆线的长度小得多，这样才可以将摆球看做质点，由摆线和摆球构成单摆．在满足偏角小于10°的条件下，单摆的周期为

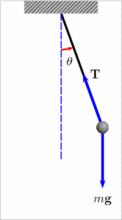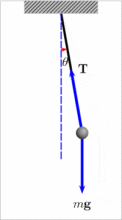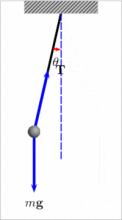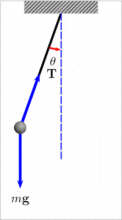
从公式中可看出，单摆周期与振幅和摆球质量无关。从受力角度分析，单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力，偏角越大，回复力越大，加速度（gsinθ ）越大，在相等时间内走过的弧长也越大，所以周期与振幅、质量无关，只与摆长l和重力加速度g有关。在有些振动系统中l不一定是绳长，g也不一定为9.8m/，因此出现了等效摆长和等效重力加速度的问题。

物理上有些问题与单摆类似，经过一些等效可以套用单摆的周期公式，这类问题称为“等效单摆”．等效单摆在生活中比较常见．除等效单摆外，单摆模型在其他问题中也有应用．

说明

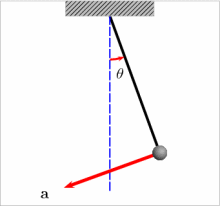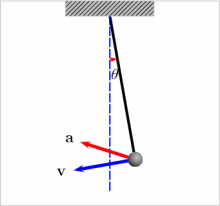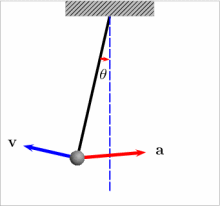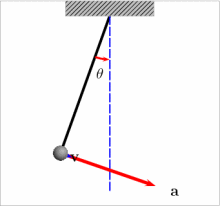单摆是质点振动系统的一种，是最简单的摆。绕一个悬点来回摆动的物体，都称为摆，但其周期一般和物体的形状、大小及密度的分布有关。但若把尺寸很小的质块悬于一端固定的长度为l且不能伸长的细绳上，把质块拉离平衡位置，使细绳和过悬点铅垂线所 成角度小于10°，放手后质块往复振动，可视为质点的振动，其周期T只和长度l和当地的重力加速度g有关，即T和质块的质量 、形状和振幅的大小都无关系，其运动状态可用简谐振动公式表示，称为单摆。如果振动的角度大于10°，则振动的周期将随振幅的增加而变大，就不成为单摆了。如摆球的尺寸相当大，绳的质量不能忽略，就成为复摆，周期就和摆球的尺寸有关了。

应用

1. 重力加速度测量：通过测量单摆的摆长和周期，可以计算出当地的重力加速度，这对于地球物理学、地质勘探等领域有重要意义。
2. 时间与频率测量：利用单摆的等时性，可以制作各种计时器和钟表，例如机械摆钟、电子钟表等，用于测量时间和频率。当单摆周期T=2s时，由公式推导，摆长大约为1m，这种情况的单摆叫做秒摆。

注意：在当前高中阶段，一般研究摆角小于10°的情况（即近似看做简谐运动），且高中阶段教材中仅涉及在实验中推测公式，不涉及单摆周期公式的推导（因为需要涉及到高等数学）。用单摆测重力加速度是单摆周期公式 的一个重要应用。1

动力学方程

由牛顿力学，单摆的运动可作如下描述。

首先可以得到，重力对单摆的力矩为

其中m为质量，g是重力加速度，l是摆长，θ是单摆与竖直方向的夹角，注意，θ是矢量，这里取它在正方向上的投影。

希望得到摆角θ的关于时间的函数，来描述单摆运动。由角动量定理知道，

其中 是单摆的转动惯量， 是角加速度。

于是化简得到

（1）

小角近似周期

（1）式是一个非线性微分方程。所以严格地说上面的（1）式描述的单摆的运动并不是简谐运动。

不过，在θ比较小时，近似地有sin θ ≈ θ。（即 。）因而此时（1）式就变为 ，这是一个二阶常系数线性齐次微分方程，其通解为 ，式中A. 为任意常数，由初值条件给定。而

于是单摆的非线性的运动被线性地近似为简谐运动

一般在高考之类的考试中，认为10°以下可以这样近似。

事实上5°≈0.087266 rad，sin 5°≈0.087155，二者相差只有千分之一点几，是十分接近的。在低精度的实验中，这种系统误差可以忽略不计（因为实验操作中的偶然误差就比它大）。但如果换成25°，误差高达百分之三，就不宜再看成是简谐振动了。

由于正弦函数的性质，这个近似是角度越小，越精确，角度越大越不精确。如果角度很大（比如60度处，误差高达17%），就完全不能说它是简谐振动了。

伽利略第一个发现摆的振动的等时性，并用实验求得单摆的周期随长度的二次方根而变动。惠更斯制成了第一个摆钟。单摆不仅是准确测定时间的仪器，也可用来测量重力加速度的变化。惠更斯的同时代人天文学家J.里希尔曾将摆钟从巴黎带到南美洲法属圭亚那，发现每天慢2.5min，经过校准，回巴黎时又快2.5min。惠更斯就断定这是由于地球自转引起的重力减弱。I. 牛顿则用单摆证明物体的重量总是和质量成正比的。直到20世纪中叶，摆依然是重力测量的主要仪器。

真实周期推导

上面提到是角度比较小的时候单摆的近似公式，但科学是严谨的，在此补充在任意角度下单摆的周期公式。

在此之前先提出两个概念（这里用Mathematica的定义）：

第一类不完全椭圆积分：

第一类完全椭圆积分：

下面用微分方程进行讨论，可以尝试用动能定理进行计算，可以更简洁地得到其特解。

设摆长为l,摆线与竖直方向的夹角为θ，那么单摆的运动公式为：

令 ，于是有 上式改写成：

这是一个可分离变量的微分方程！分离变量：

其通解为

给定初始条件 （0≤α≤π）， ，则其特解为：

所以考虑t（t是四分之一周期）：

设 ，则

又考虑到

便可以化简得到

按照前面的定义，便有

此处的α就是常说的摆角。

相关差别

直观差别图如右：

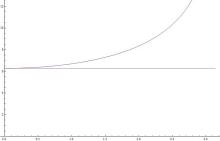利用电脑软件，列出近似公式与真实公式的差别。

下面数据皆是相对误差：相对误差=（真实值-近似值）/真实值

每一行，摆角相差1度，自0取到180度。

0

0.0019038558531896002%

0.0076153871712633745%

0.01713448526148856%

0.030460969075184717%

0.047594585366650885%

0.06853500891589595%

0.09328184281540482%

0.12183461882124084%

0.1541927977688524%

0.1903557700540208%

0.23032285617945628%

0.27409330736761933%

0.32166630624041737%

0.37304096756649924%

0.42821633907694606%

0.48719140235023334%

0.549965073767417%

0.6165362055385787%

0.686903586801647%

0.7610659447947971%

0.839021946103721%

0.92077019798515%

1.006309249768103%

1.0956375943344412%

1.188753669680396%

1.2856558605608566%

1.386342500218304%

1.490811872198394%

1.599062212254311%

1.7110917103421366%

1.8268985127096076%

1.9464807240807704%

2.0698364099391786%

2.1969635989124314%

2.3278602852610035%

2.4625244314744745%

2.600953970978439%

2.7431468109555626%

2.8891008352844154%

3.038813907599942%

3.192283874479603%

3.3495085687594606%

3.5104858129847005%

3.675213422999331%

3.843689211680047%

4.0159109928195225%

4.191876585164665%

4.371583816615697%

4.555030528592199%

4.742214580572629%

4.933133854814164%

5.127786261260084%

5.326169742642323%

5.5282822797872475%

5.734121897133129%

5.9436866684683%

6.156974722899461%

6.3739842510601274%

6.594713511569824%

6.819160837755173%

7.04732464464473%

7.279203436250061%

7.514795813146305%

7.754100480366246%

7.99711625562274%

8.243842077875229%

8.494277016257039%

8.748420279381131%

9.006271225043092%

9.2678293703413%

9.533094402235417%

9.802066188565687%

10.074744789556986%

10.351130469833013%

10.63122371096772%

10.915025224602775%

11.202535966161768%

11.493757149193899%

11.788690260382037%

12.087337075252421%

12.389699674625776%

12.695780461852351%

13.00558218087636%

13.319107935178396%

13.636361207647948%

13.957345881441757%

14.282066261887804%

14.610527099499105%

14.942733614166162%

15.278691520602091%

15.61840705511994%

15.961887003827869%

16.309138732334322%

16.660170217062607%

17.014990078281997%

17.373607614971124%

17.7360328416386%

18.10227652723615%

18.472350236310504%

18.846266372552723%

19.224038224916786%

19.605680016494205%

19.991206956347447%

20.380635294522822%

20.773982380483087%

21.171266725221678%

21.57250806734433%

21.977727443430435%

22.386947263015642%

22.800191388569722%

23.21748522087999%

23.63885579029045%

24.06433185429185%

24.493944002007527%

24.92772476617582%

25.365708743292277%

25.807932722644754%

26.254435825053335%

26.70525965221522%

27.160448447654655%

27.62004927039044%

28.08411218256101%

28.552690452391587%

29.025840774051932%

29.50362350614023%

29.986102930741776%

30.47334753525516%

30.965430319458193%

31.462429130607322%

31.96442702973461%

32.47151269273426%

32.98378085032637%

33.50133277156177%

34.0242767962028%

34.552728922099824%

35.086813454603366%

35.62666372613477%

36.17242289531702%

36.72424483658309%

37.282295132982576%

37.84675218706157%

38.41780846727546%

38.99567191050804%

39.58056750504079%

40.172739082901636%

40.77245135613077%

41.37999223839477%

41.99567550190461%

42.61984383019676%

43.25287234061159%

43.895172667035965%

44.54719771472042%

45.20944722616039%

45.88247433208869%

46.56689330724679%

47.263388810526784%

47.972726968588255%

48.69576876871157%

49.433486371410815%

50.18698315232789%

50.95751856030661%

51.7465392710714%

52.55571868071775%

53.38700761086381%

54.24270033499423%

55.12552192866632%

56.03874591621829%

56.986355981090206%

57.97327350290041%

59.00568652891076%

60.09154082585585%

61.24130132912596%

62.46918883739732%

63.795307588848516%

65.24958544634976%

66.87982354979094%

68.77058140504862%

71.09802414324294%

74.36597547372776%

100%

来源: 百度百科

内容资源由项目单位提供