定义

等价无穷小的定义：设当 时， 和 均为无穷小量。若 ，则称 和 是等价无穷小量，记作 。

例如：由于 ，故有 。

等价无穷小替换是计算未定型极限的常用方法，它可以使求极限问题化繁为简，化难为易。

求极限时，使用等价无穷小的条件1：

1. 被代换的量，在取极限的时候极限值为0；
2. 被代换的量，作为被乘或者被除的元素时可以用等价无穷小代换，但是作为加减的元素时就不可以。

性质

当，就说 β与α是等价无穷小。4

常见性质有：设α，α'，β，β'，γ等均为同一自变量变化过程中的无穷小。4

1. 若α~α'，β~β'，且存在，则4
2. 若α~β，β~γ，则α~γ4

性质1表明等价无穷小的商的极限求法，性质2表明等价无穷小的传递性。4

定理

无穷小等价替换定理2

设函数 ， ， ，在 内有定义，且有

(1)若 ，则 ；

(2)若 ，则 。

证明：

(1) 。

(2)。

例如：利用等价无穷小量代换求极限

解：由于，

而，， ，

故有。

注意：等价无穷小一般只能在乘除中替换，在加减中替换有时会出错（加减时可以整体代换，不一定能随意 单独代换或分别代换）1。如在上例中：

若因有，，而推出 ,则得到的是 错误的结果。

注：可直接等价替换的类型

（以上几个性质可以用来化简一些未定式以方便运用洛必达法则）

需要满足一定条件才能替换的类型

若 ，则

（该条性质非常重要，这是判断在加减法中能否分别等价替换的重要依据）

变上限积分函数（积分变限函数）也可以用等价无穷小进行替换。

公式

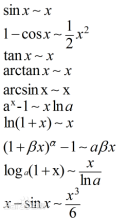当 时，

注：以上各式可通过泰勒展开式推导出来。

推导过程

α和β都是无穷小，且，存在（或

来源: 百度百科

内容资源由项目单位提供