点到平面的距离计算方法

计算一点到平面的距离，通常可通过向量法或测量法求得。

向量法

向量在轴上的投影

设 、 两点在 轴上的投影分别为 、 ，则向量 的长度 称为向量 在 轴上的投影，记为 。设 与 轴之间夹角为 ，则

在计算点到平面的距离时将用到上述公式。1

点到平面的距离计算

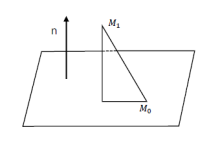向量法计算点到平面的距离，就是把点和平面放在直角坐标系下进行计算。这样，点和平面均可用坐标来表示（如图1所示）。

设平面 的方程为：

设向量 为 的法向量，平面外一点 坐标为 ，在平面上取一点 ，则点 到平面 的距离 为：

其中 为向量 与向量 的夹角，

故

而

由于点 在平面上，因此有

即 由此可得

所以

此公式即为点到平面的距离公式。1

测量法

过平面外一点做平面的垂线，点到垂足的距离就是点到平面的距离。1

求解策略

点到平面的距离问题是立体几何中的常见问题，是求直线与平面所成的角、二面角以及几何体的体积的基础．对这类问题，需灵活掌握以下求解策略：2

1.直接作出平面的垂线；2

2.寻找两个垂直平面，在一个平面内作交线的垂线；2

3.利用直线与平面平行时，直线上任何一点到平面的距离都相等的这一性质，转化为求直线上另外一点到平面的距离；2

4.过该点作平面的斜线段：转化为求该线段的中点到平面的距离；2

5.利用三棱锥的等积变换一体积法。2

来源: 百度百科

内容资源由项目单位提供