理解黎曼猜想（五）跟外星文明交流，第一条信息应该发什么？

导读

无论任何行星，任何星系，甚至任何维度，数学的规律都不会变。想想看，除了质数之外，还有什么更适合作为跟外星文明交流的第一条信息呢？质数跟我们经常强调的可控核聚变一样，都是宇宙级别的关键科技！在这个意义上，可以把黎曼猜想理解为宇宙的密码！

本文为黎曼猜想系列之四，

黎曼猜想（一）见黎曼猜想（一）每出现一个数学公式，就会吓跑一半观众？如何打破“跳蚤效应” | 科技袁人，

黎曼猜想（二）见黎曼猜想（二）两个自然数互质的概率是多少？我不仅算起黎曼猜想，还写了个程序 | 科技袁人，

黎曼猜想（三）见黎曼猜想（三）你真的相信全体自然数的和等于-1/12吗？| 科技袁人

黎曼猜想（四）见黎曼猜想（四）短短8页纸，至今仍在给数学家启发和挑战，黎曼究竟写了什么？| 科技袁人

精彩呈现：

在上一期节目中，我们知道了一个根本性的结论：质数分布的全部信息，都包含在黎曼ζ函数非平凡零点的位置之中。然后，我们介绍了黎曼猜想的内容。它说的是：黎曼ζ函数所有的非平凡零点，实部都等于1/2。数学家经常把黎曼ζ函数非平凡零点的实部和虚部分别写成σ和t，把复平面上0 < σ < 1的竖直条带称为临界带，把σ = 1/2的竖线称为临界线。我们已经知道的是，黎曼ζ函数所有的非平凡零点都位于临界带内部。而黎曼猜想说的就是，黎曼ζ函数所有的非平凡零点都位于临界线上，在临界线外一个都没有。

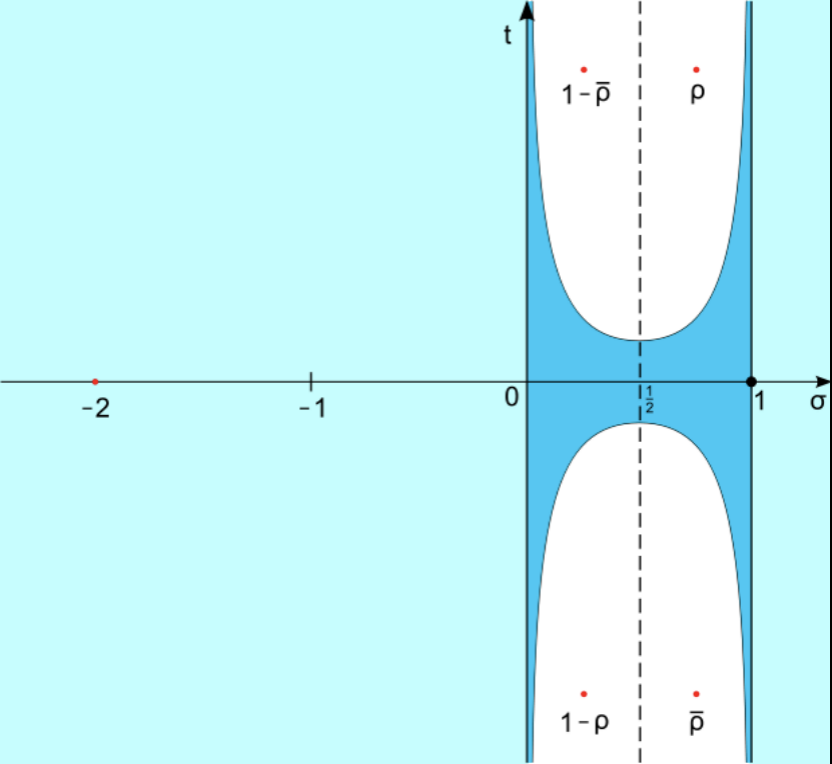
临界线与临界带

在继续介绍之前，让我们来回答一个许多人问起的问题：质数有什么用？我欣慰地看到，不少同学们都主动地做出了回答：质数在密码学中有十分重要的应用。例如当今世界最常用的密码体系之一叫做RSA，这个名字是三位发明者的姓的首字母缩写。RSA密码体系的基础就是因数分解的困难性，即把一个很大的合数分解成两个质数的乘积需要非常大的计算量。同学们的这种主动精神非常好！我还可以补充一点质数在机械方面的应用：齿轮的齿数经常被设计成质数。为什么呢？因为这样可以使两个齿轮的两个齿在两次相遇之间的啮合次数最大化，使磨损均匀化，增加耐用度，减少故障。

《三体》英文版封面质数在日常生活中的应用固然很有趣，不过我还想再谈一个宇宙层面的应用，就是作为智慧的标志。在《三体》的第三部《死神永生》中，人类的太空艇探险队和四维空间的文明进行了这样的交流：

“按照计划，卓文用中频电波发送了一个问候语。这是一幅简单的点阵图，图中由六行不同数量的点组成了一个质数数列：2、3、5、7、11、13。他们没有指望得到应答，但应答立刻出现了，速度之快让三人不敢相信自己的眼睛。悬浮在太空艇舱里的信息窗口显示出一个简单点阵图，与他们发送的类似，也用六行点组成六个质数，但图中的点阵大了许多，把他们发送的那个数列接了下来：17、19、23、29、31、37。对方的含义很明确，回答了他们的问候。”

这在科幻小说中，是很标准的设定。无论任何行星，任何星系，甚至任何维度，数学的规律都不会变。而在数学中又属自然数最为简单，而在自然数中又属质数最容易表现出智慧含量。想想看，除了质数之外，还有什么更适合作为跟外星文明交流的第一条信息呢？心事浩茫连广宇，于无声处听惊雷。质数跟我们经常强调的可控核聚变一样，都是宇宙级别的关键科技！在这个意义上，可以把黎曼猜想理解为宇宙的密码！上次我们说到，黎曼对小于等于x的质数个数即质数计数函数π(x)，推出了下面的表达式，其中唯一未知的就是那些非平凡零点的位置ρ：

1896年，在1859年提出黎曼猜想的37年之后，阿达马和德·拉·瓦·布桑证明了质数定理，并因此续到了90多岁。质数定理说的是，质数计数函数π(x)约等于对数积分函数Li(x)，也约等于x/lnx。

质数定理的相对偏差

因此，我们对质数的分布可以这样理解：质数定理给出了π(x)的基本轮廓，即Li(x)，黎曼ζ函数的非平凡零点给出了π(x)对这个轮廓的修正。而对于这个修正，黎曼猜想又给出了它的最重要的特征。

什么样的特征呢？我们可以注意到，对于一个复数ρ = σ + it，x的ρ次方的绝对值是由ρ的实部也就是σ决定的，因为ρ的虚部也就是t只影响x的ρ次方的方向，而不影响其大小。我们还可以注意到，在x很大时，对数积分函数Li(x)约等于x/lnx，而lnx的增长速度比x慢得多，因此Li(x)的增长速度大约就是x。因此，如果黎曼猜想成立，也就是说所有的σ都等于1/2，那么所有这些Li(xρ)加起来的增长速度就大约是x的1/2次方，即根号x。

你也许会问，无穷多个根号x加起来，难道不会发散吗？回答是，别忘了ρ还有虚部呢，它会使x的ρ次方的矢量旋转。因此不同零点的贡献会在很大程度上抵消，最后得到一个有限的值，而这个有限值的长度正比于根号x。

如果黎曼猜想不成立，也就是说有些σ不等于1/2，会产生什么后果呢？如果有一个非平凡零点的σ > 1/2，也就是说它位于临界线右侧，那么它就会导致Li(xρ)的增长速度超过根号x。当x无限增大时，这一个零点的贡献就会淹没所有的临界线上的零点的贡献。好比你跟一群人赛跑，你的速度是x的2/3次方，他们的速度是x的1/2次方，那么当x充分大的时候，必然会导致他们跑过的路程加起来都没有你多。因此，这一个右侧的零点就会使得π(x)对Li(x)的偏离的增长速度超过根号x。

而如果有一个非平凡零点的σ < 1/2，也就是说位于临界线的左侧呢？别忘了，非平凡零点对于临界线是对称的。所以如果有一个在左侧，就必然会有一个相应的在右侧。因此，只要有一个非平凡零点不在临界线上，就会导致π(x)对Li(x)的偏离的增长速度超过根号x！我们强调一下：只要有一个非平凡零点不在临界线上，就足以导致可观的后果了！

因此黎曼猜想意味着，在质数分布对其轮廓所有可能的偏离中，实际取到的是最小的偏离。这是一个多么深刻的猜测！现在你明白黎曼猜想的意义何在了吧？

例如美国数学家舍恩菲尔德（Lowell Schoenfeld，1920 - 2002）在1976年证明了，如果黎曼猜想成立，那么下列不等式对任何大于等于2657的x都成立：

而如果不以黎曼猜想作为前提，那么我们对|π(x) - Li(x)|的增长速度能够证明的，就只是它不超过x。这跟黎曼猜想对应的结果根号x相比，就差得太多了！

人们已经发现了许多跟黎曼猜想等价的猜想。例如1984年，有一位法国数学家Guy Robin就证明了一个。这位法国数学家的姓Robin用英语读出来像“罗宾”，但用法语读出来更像“猴棒”，猴赛雷的猴，金箍棒的棒，真是太棒了。根据名从主人的原则，我们还是称呼他“猴棒”吧。总之，猴棒证明了，黎曼猜想等价于下列不等式对任何大于等于5041的自然数n都成立：

这里的γ是欧拉常数，我们在本系列的第二篇中介绍过，约等于0.577216。而σ(n)是因数和函数（sum-of-divisors function），意思是一个自然数n的所有因数之和，包括1和这个自然数本身在内。例如12的因数包括1、2、3、4、6、12，σ(12)就等于1 + 2 + 3+ 4 + 6 + 12 = 28。

受到黎曼猜想的启发，人们在数学的若干其他领域也提出了类似的猜想。这些猜想都可以理解为黎曼猜想的推广，这些推广也对数学产生了深远的影响。

我的朋友卢昌海博士写了一本非常好的科普著作《黎曼猜想漫谈》（清华大学出版社2012年8月第一版），得到了许多图书奖。著名的数学家、前中国数学会理事长王元院士给此书撰写了序言，向大众推荐此书。王元院士写道：

“就像研究FLT（按：Fermat’s last theorem，费马最后定理）与GC（按：Goldbach's conjecture，哥德巴赫猜想）一样，研究它们的目的主要在于发展数学中的新思想与新方法。形象地说，这两个问题都是数学中的‘下金蛋的母鸡’。

从过去的研究来看，RH（按：Riemann hypothesis，黎曼猜想）当然是数学中下金蛋的母鸡，但研究它的目的，远远不止此。它之所以成为数学中第一重要问题，主要是由于一系列的数学中的重大问题的解决都依赖于各种RH的解决。一旦这些RH解决了，人类就站在一个不知比现在高多少的数学平台上，看到更远得多的风景。”

《黎曼猜想漫谈》

请看，王元对黎曼猜想的评价是，“数学中第一重要问题”！如果我们保守一点，那么说黎曼猜想是“数学中最重要的问题之一”，则是完全没有疑问的。

王元院士

黎曼猜想在公众中的知名度，在很大程度上来自两次世纪之交时的宣传。

第一次是在1900年，伟大的德国数学家希尔伯特（David Hilbert，1862 - 1943）在国际数学家大会上提出了经典的23个数学问题，对后世产生了深远的影响。其中第八个问题就是“黎曼猜想与其他质数问题，包括哥德巴赫猜想和孪生质数猜想”。事实证明这三个猜想都是特别难的问题，直到现在都没有解决。

希尔伯特

第二次是在2000年，克雷数学研究所（Clay Mathematics Institute）提出了七个“千年大奖问题”（Millennium Prize Problems），对每一个问题的解决悬赏一百万美元。其中第四个问题就是黎曼猜想。人们笑谈，这是世界上最难的获得一百万美元的方法！

克雷数学研究所的这七笔悬赏发出去了几笔呢？回答是：一笔都没发出去。到目前为止，这七个问题中只有一个被解决了，就是第三个问题“庞加莱猜想”（Poincaré conjecture）。但是，解决者俄罗斯数学家佩雷尔曼（Grigori Yakovlevich Perelman）不屑于去领奖！这位长得有点像沙僧的哥们是个神人，以后我们有机会再来介绍他。

佩雷尔曼

虽然有这么两次大规模的宣传，不过论起在公众中的知名度，黎曼猜想还是显著的落在哥德巴赫猜想与孪生质数猜想后面。这是因为后两者的表述非常简单，小学生都能看懂，而黎曼猜想的表述就复杂得多，需要有复变函数的知识才能理解。简单地说，哥德巴赫猜想和孪生质数猜想很容易“扮猪吃老虎”，而黎曼猜想一看就知道是老虎。这倒也未尝不是一件好事，至少号称自己攻克了黎曼猜想的民科，就比号称自己攻克了哥德巴赫猜想或者孪生质数猜想的民科少得多！

但如果论起在数学上的重要性，顺序就反过来了。从王元的序言，我们可以理解，不少著名猜想的重要性主要在于启发新思想，本身的用处比较小。而黎曼猜想不但能启发新思想，而且本身的用处就非常大。因此，黎曼猜想虽然与哥德巴赫猜想、孪生质数猜想同列于希尔伯特第八问题，但重要性还是比它们高一个层次。

当然，我们并不是说哥德巴赫猜想与孪生质数猜想不重要，也不是说陈景润与张益唐的工作不重要。哥德巴赫猜想与孪生质数猜想都是非常重要的问题，而且它们挑战人类智力的时间比黎曼猜想还要长。陈景润与张益唐的相关工作都是非常杰出的成果，值得我们高度的敬佩与赞誉。我们只是希望读者明白，这些不是数学的全部，世界上还有其他的而且是更重要的问题需要关注。

对于专业数学家来说，他们都十分清楚黎曼猜想的重要性。例如有人曾经问希尔伯特，如果他能在500年后重返人间，他最想问的问题是什么？希尔伯特回答说，他最想问的就是：是否有人解决了黎曼猜想？

来，让我们为希尔伯特献上一首《向天再借五百年》！

《向天再借五百年》

这里有一点值得提的是，许多人在知道了密码学和黎曼猜想都与质数有关之后，认为如果黎曼猜想被证明了，许多密码体系就会被破解。我们必须指出，这是一种过度解读。

实际上，从来没有哪个密码体系是以黎曼猜想的成立或者不成立作为设计基础的。例如RSA，它的基础是因数分解的困难性。如果我们证明了黎曼猜想，那么当然会对质数的分布增加很多了解，但这是否会导致更快的因数分解算法呢？至少目前没有，将来有没有不知道。这是一个假设性的问题，到时又会需要很多的研究。因此，黎曼猜想和密码学之间的联系，只是一种间接的联系，而不是立竿见影、一触即发的直接联系。

对黎曼猜想的意义和重要性了解了这么多，那么人们尝试证明黎曼猜想的努力，达到什么程度了呢？

基本的回答是：离真正解决问题，看起来还离得远。具体的进展情况，我们下次来讲。

下一期将是本系列的最后一期，技术性内容将会很少，而故事性与情怀性内容将会很多，相信所有的同学们都能有所收获哦~

来源: 风云之声

内容资源由项目单位提供