上节我们介绍了CPU的基本单元是晶体管开关，接下来我们就看看这一堆开关组合在一起能做什么？首先我们需要用晶体管开关制作几种最基本的建筑材料——门电路。

这有一个晶体管开关，我们在输入端添加一个通道（细线），这条线比其他线更细，留意这点。

然后我们人为规定控制端为输入端，新加的细线为输出端。

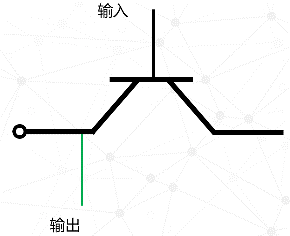
请注意，虽然晶体管本身有固定的输出、输出、控制端，但作为使用者我们完全可以根据需要调整输入端、输出端的定义，只要输入端的变化能引发输出端变化即可。

接下来我们分析输入和输出端之间的关系，当输入端是0（0代表没电，1代表有电），主通道关闭，从左边过来的电流无法到达右边，但可以经这条细线流出，所以输出是1。即输入是0，输出是1。

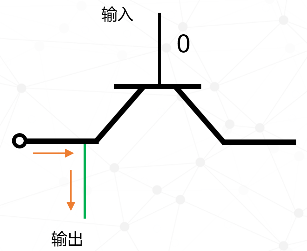
接下来输入是1的话，主通道打开，电流从左边流到右边，因为主通道通了，输出端（细线）就没有电流了。

我们可以做个类比，某天早晨打开水龙头，发现没水，一看新闻，原来市政主管道被挖断了，路面上都能游泳了，所以家里就没水了，这是同样的道理，因为水都从主管道流走了，家里的小管道自然就没水了。所以输入是1，输出是0。

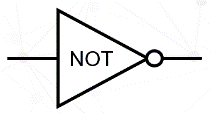
我们用一个表格记录输入、输出之间的关系，会发现它们之间存在相反的关系，所以这个简单的电路称为非门电路，非就是相反的意思，门是一个形象的解释，就好像一个开关，门打开，人能进出，门关上，谁也不能进出。这个非门电路以后我们经常用到，为了简单起见，我用一个符号代表这个电路。其中的NOT就是非的意思。

然后我们看第二个门电路，这有二个晶体管开关，把他们首尾相连，然后将两个晶体管的控制端当做输入，分别叫输入A、输入B，最后一个晶体管的输出端当做输出。

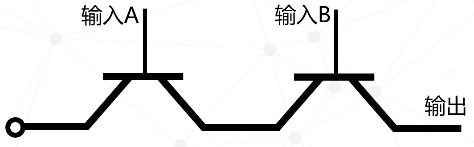
然后分析下输入和输出的关系，当输入A=0，输入B=1时，第一个开关主管道关闭，第二个开关主管道打开，电流无法从左边流到右边，输出=0；当输入A=1，输入B=0时，也是类似，输出=0；当输入A=0，输入B=0时，输出当然=0；而当输入A=1，输入B=1时，二个开关都打开，输出=1。

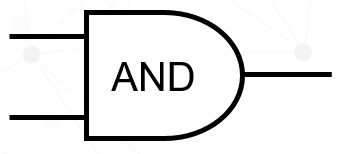
用表格整理一下，会发现一个规律，只有当A、B都是1的时候输出才是1，可以用一句话描述“当输入A=1并且输入B=1时，输出才=1”，其他的情况输出都是0。这个电路称为与门电路，与就是并且的意思。这个门电路以后会经常用到，也用一个符号代表，其中AND就是与的意思。

接下来再用二个晶体管彼此相连，但不是串联，而是并联，也就是两个输入端连在一起，两个输出端连在一起。

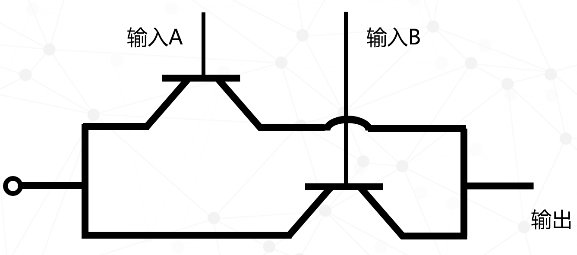
注意，图中那个圆弧代表二条线不是相连，因为在平面上无法画出立体图，大家可以想象一下，二条线一个在上一个在下，没有任何接触。现在我们将两个晶体管的控制端分别当做输入A、输入B，输出端不变，接下来分析输入输出之间的关系。

当输入A=0，输入B=1时，下面这个晶体管打开，电流可以走下面通道从输出端流出，输出=1；当输入A=1，输入B=0时，上面这个晶体管打开，电流可以走上面通道从输出端流出，输出=1；当输入A=0，输入B=0时，二个晶体管都关闭，输出=0；当输入A=1，输入B=1时，两个通道都打开，输出=1。

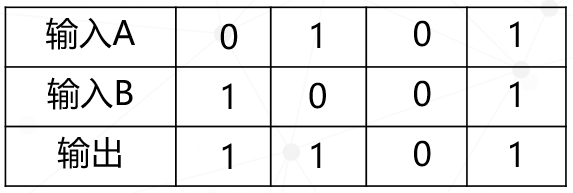
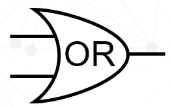
使用表格总结一下，会发现这样一个规律：“只要输入A或者输入B有一个为1，输出就=1”，这个门电路称为或门电路，为了方便描述，使用这个符号代替或门电路，其中or就是或者的意思。

有了上面三种最基本的门电路，我们就可以组合出更复杂的门电路（姑且称为二阶门电路，与基本门电路区分），种类很多，比如与非门、或非门、异或门等等，我们举其中一个例子——异或门。电路是这样的，由二个与门、一个非门、一个或门组成。

电路分析用下面四张图来表示，大家可以自己推理一下，看结果是否正确。

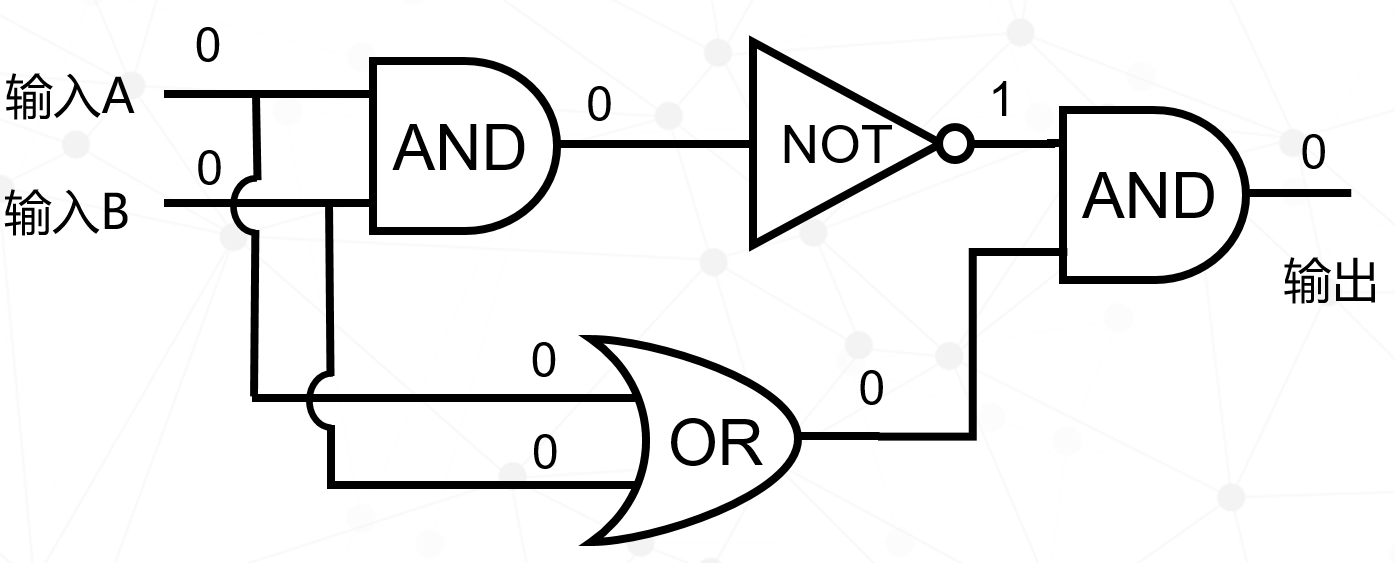
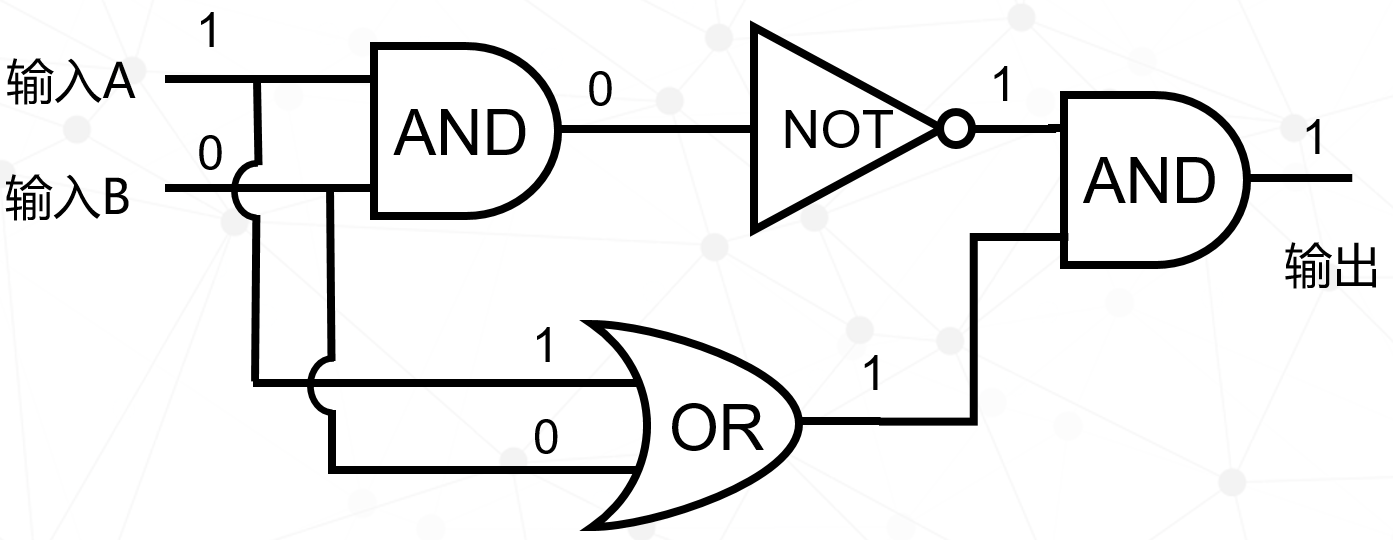
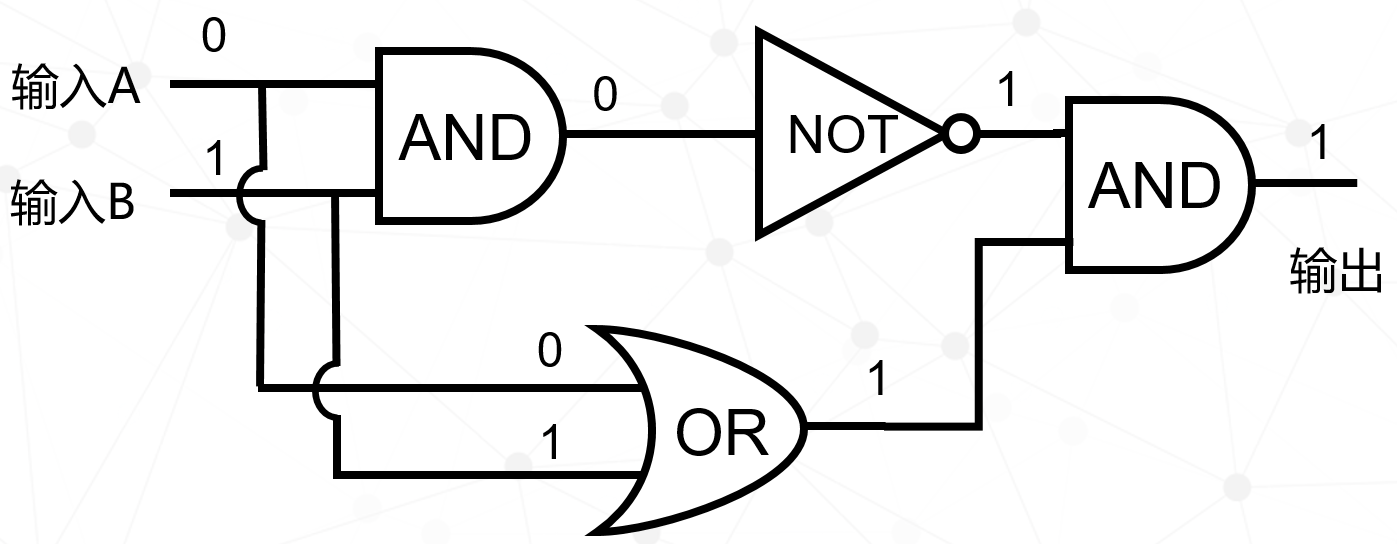
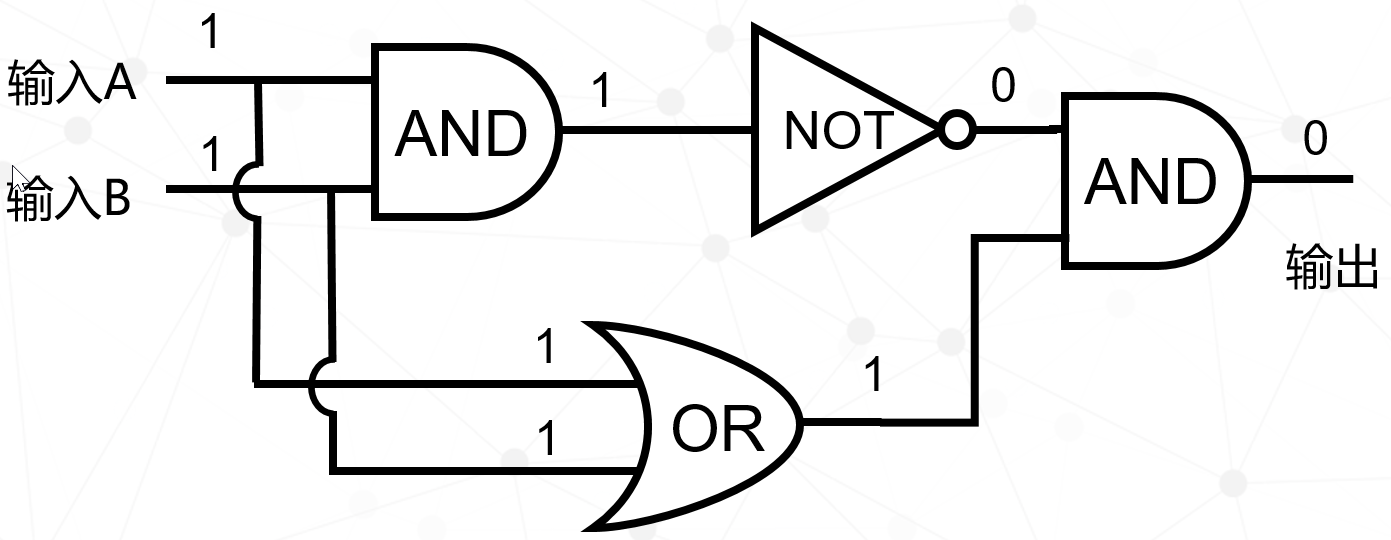
最后用表格统计出来：

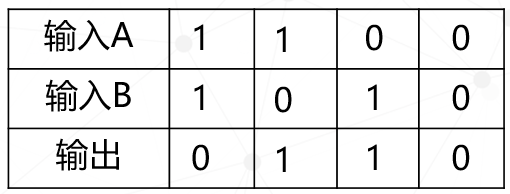
它的规律是：当输入A和输入B不同时，输出=1。我们用这个符号来描述异或门。

其他二阶门电路我们不一一介绍了，有兴趣的读者可以自己查阅资料，下节我们来看看由这些门电路如何制作加法器，实现加法运算。

来源: 孙老师聊人工智能