一、复杂世界，简单规则

夕阳下，鸟儿成群舞动，时而疏散，时而聚拢，不断变化着空间排序却能互不相撞，既能飞越障碍也不会彼此失散。鸟群如何在空中舞蹈、鱼群如何在水中变幻？

2021年，一艘货轮意外在苏伊士运河搁浅，给全球经济带来“多米诺骨牌”式影响，每天由此减少的贸易额高达90亿美元，为什么小小一艘货轮能堵住全球供应链？同样地，为什么一条网络谣言可以引爆全网大规模舆情？难道一只蝴蝶轻轻振翅，真能卷起千里之外的一场风暴吗？

这些问题看似毫不相关，但仔细思考就会发现，这些复杂现象均有一个共同点：它们都发生在由大量主体通过相互作用构成的复杂系统中。2021年诺贝尔物理学奖颁发给了意大利物理学家乔治·帕里西教授（Giorgio Parisi）以表彰他对复杂系统理论的开创性贡献。年轻时的乔治·帕里西教授也曾在罗马火车站，对空中成千上万只鸟儿成群飞翔的景象着迷。他常伫立良久，观察、拍摄鸟群。基于对鸟群的观察数据，帕里西教授用统计物理方法揭开了鸟群飞行的奥秘[1]。原来每只鸟只需要遵循三个最基本的原则，就可以复现鸟群飞翔的奇景。这三个基本原则为：

（1）靠近视野中的邻居，每只鸟都希望与视野中的同伴携行；

（2）与视野中的邻居保持一致的飞行方向；

（3）当与邻居过于靠近时，调整方向，避免碰撞。

所以，鸟群飞行的奥秘不在于每只鸟，而是它们之间的相互作用。鸟群飞行如此复杂，但背后规则竟如此简单！研究鸟群这样的系统时出现一个魔咒：我们惯于依赖的还原论[ 还原论（Reductionism）是一种哲学思想，认为复杂的系统、事物、现象可以将其化解为各部分之组合来加以理解和描述。]失效了。

二、什么是复杂系统？

还原论虽然不能理解鸟群的集体行为，但对理解飞机就很有效，尽管飞机的零件也不计其数，功能也眼花缭乱，但只要我们明白每个零件的作用，就能完全理解飞机的飞行原理。我们称飞机这样的系统为复合系统（Complexed systems），而像鸟群、大脑这样的系统，即使我们研究清楚了系统的所有组成部分（如每只鸟、每个神经元），也无法理解系统整体涌现的奇观（如鸟群飞舞、意识涌现），这样的系统就是复杂系统（Complex systems），如图1所示。复杂系统研究旨在解决的核心问题就是探索复杂系统背后的简单、普适规律。

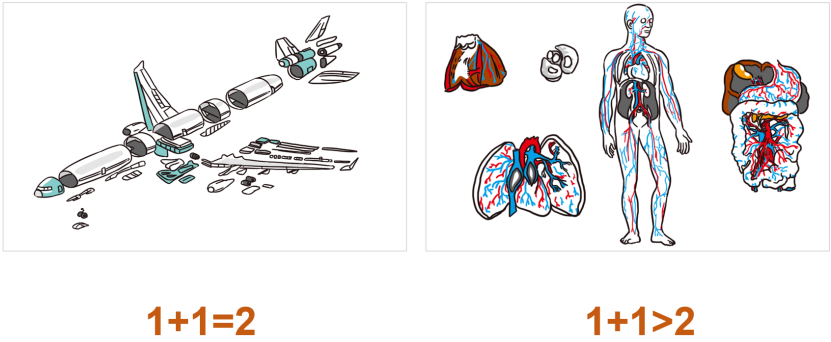
图1 复合系统与复杂系统

牛顿建立了机械性、确定性的物理王国。像小球从斜面滑下的故事时刻都被牛顿力学牢牢控制。在这个确定性王国里，只要我们给定了系统的初始状态，那万物都将按照确定的规则运行。1961年的冬天，气象学家洛伦茨（Edward Norton Lorenz）构建了一个精巧的数学模型，希望能预测天气，却意外地发现了另一个世界。计算机千分之二的系统误差（0.0001秒）竟会得到截然不同的结果。所谓“差之毫厘，谬以千里”。他把这个高度非线性的天气模型输入到计算机中，得到的状态轨迹竟像一只张开翅膀的蝴蝶。于是就有了大家非常熟悉的蝴蝶效应（如图2所示），这一效应形象地表现了非线性系统对初值的敏感性，也体现了复杂系统一个有趣的现象——混沌。

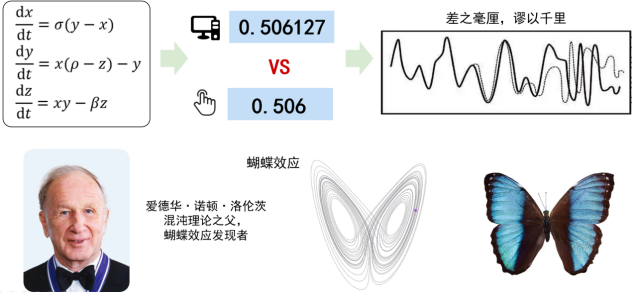
图2 蝴蝶效应起源

实际上，大多数我们熟悉的真实系统，既不是混沌的，也不是完全秩序的，而是处于两者之间，我们称之为混沌与秩序的边缘状态。复杂性科学正是诞生于混沌与秩序边缘的科学。1984年，在盖尔曼、安德逊和阿罗等人的支持下，一批从事物理、经济和计算机领域的科学家在圣塔菲伊苏区中一个租来的女修道院中组建了圣达菲研究所（Santa Fe Institute）。该研究所如今已经成为世界知名的复杂科学研究中心。以圣塔菲研究所成员为代表的一大批学者，尝试突破牛顿以来的还原论思维桎梏，理解涌现、混沌等复杂系统现象。

三、如何探索复杂世界的简单规则——网络科学

圣塔菲研究所的创始人之一乔治·考温曾说，他们正在开创二十一世纪的科学。如今，未来已来！经过科学家们三十多年来的努力，如今复杂科学又迎来了一个新发展阶段——应用复杂网络来刻画、研究复杂系统。网络科学应运而生。网络科学的核心思路，就是应用复杂网络对各类复杂系统进行建模[2]。在现实世界中，大到全球生态系统和全球物流系统，小到细胞内的蛋白质交互系统，都可以用复杂网络进行建模（如图3所示），其中节点表示系统的组成元素，连边表示元素之间的相互作用，通过研究系统抽象而成的网络结构及其上的动力学，就可以理解网络所对应的复杂系统的规律。

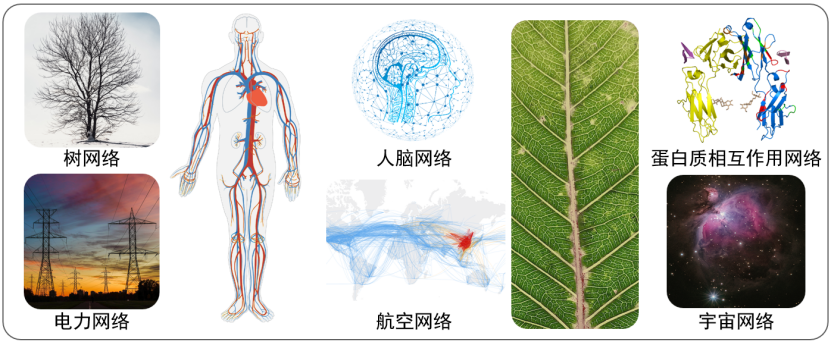
图3 多种复杂网络实例

[ 蛋白质相互作用网络来自www.creative-proteomics.com]

社交网络是我们日常生活中最为熟悉的网络，每个人作为社交网络中的节点，通过线上线下关系联系起来。回到刚开始的问题，为什么一条网络谣言可以引爆全网大规模舆情，我们又应该从何入手、控制舆情呢？解决这些问题的关键在于在社交平台上找到谣言传播过程中的关键人物，以及识别和切断重要的传播路径。归结起来就是对两个关键科学问题的探索：如何挖掘网络中的重要节点[3]，以及如何挖掘网络中的重要链路[4]。这两个问题的研究在网络科学中被称为网络信息挖掘（如图4所示）。

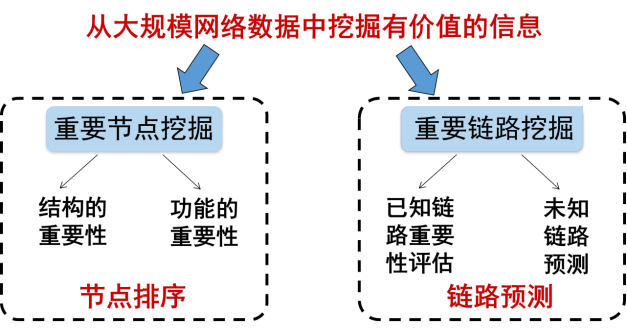
图4 网络信息挖掘

1. 如何挖掘网络中的重要节点？

对于第一个科学问题：如何基于已知的网络信息挖掘出对网络结构和功能产生重要影响的节点，其实是如何对节点进行排序的问题。在解决这一问题的方法中，依据节点的核数进行排序是一种经典的方法（即K-core分解[5]），它刻画了节点在网络中的位置。这就像一个剥洋葱的过程，把网络一层一层剥掉，越晚剥掉的节点处于网络中的核心位置，这个节点的影响力也就越大。但这样的方法大多适用于静态的、简单的网络。而在现实生活中我们面对的网络大多数都是大规模、含权、演化、有向的。面对这样的复杂网络时，我们又该如何快速高效地计算核数，挖掘出重要节点呢？

受到科学家H指数的启发，我们定义了一个局部H算子[6]，将算子H作用在有限的实数序列上，得到y=H(x1,x2,...,xn)。H算子的定义为在实数序列（x1,x2,...,xn），最多找到y个不小于y的数（如图5所示），这个概念与H指数的概念完全一致。当我们把H算子作用在网络的节点度序列上时，返回的y值就称为该节点的一阶H指数，将H算子进一步作用在某节点的邻居的一阶H指数上时，可以得到该节点的二阶H指数。经过这样连续的作用，就能得到节点的H指数序列。有趣的是，这个序列可以被严格证明为收敛于节点的核数。

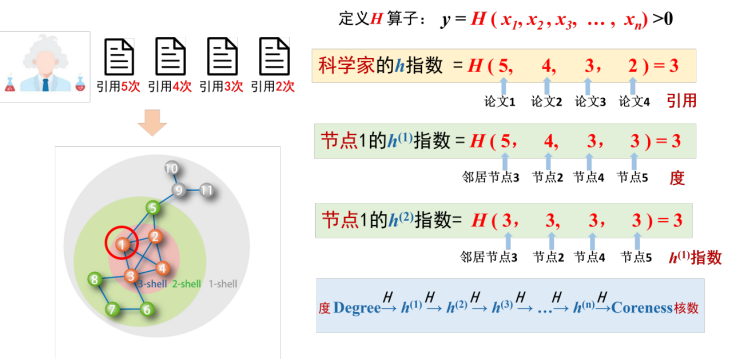
图5 H算子定义示意图

因此，通过H算子，我们把长期以来被认为毫不相关的三个指标：度、H-指数与核数联系了起来，我们称这一发现为网络的DHC定理[6]（如图6所示）。这个定理对于演化、含权、有向网络同样适用。基于该定理就可以通过分布式的方式仅基于网络节点局部的信息快速计算节点的核数，从而快速准确地挖掘出复杂网络中的重要节点。

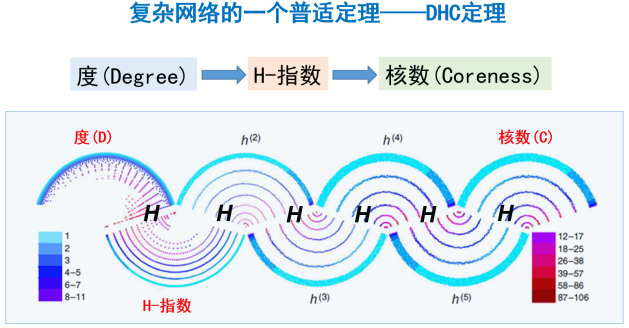
图6 DHC定理

我们发现，在微博网络中应用DHC定理去识别关键用户，只需要监测不到四万分之一的微博用户就可以跟踪95%以上的重大食品安全舆情。此外，这一方法还可以应用在国家创新力分析[7]、重要脑区识别[8]、城市媒体影响力分析[9]等多个领域中。

2. 如何挖掘网络中的隐含链路？

对于第二个科学问题，如何基于已知的网络结构信息和可能的节点属性信息，估计两个未连接节点之间产生连接的可能性？这个问题被称作链路预测，社交网络中的“好友推荐”就是典型的链路预测问题的应用。在链路预测研究中，数据和算法直接决定了预测精度。当获得一个较差的预测结果时，我们就往往会探究怎么设计更好的算法。但却忽略了一个非常关键的问题：分析的数据本身是否是可预测的，即如何刻画网络数据的可预测性。

我们认为，如果随机从网络中抽取出一小部分链路，网络的特征向量空间受到的影响很小，就说明网络是具有规律性的，即可预测性高的。在这种思路的基础上，我们应用类似于量子力学中对哈密顿量做一阶微扰的方法，假定减少或者加入少量链接所产生的微扰，只对特征值有影响，而对特征向量没有影响，这样就可以观察微扰后通过这种办法重构的邻接矩阵和真实邻接矩阵的差异。我们提出了一个度量这种差异的指标——网络的结构一致性[10]。一致性越强则表示该网络的可预测性越大。依据这个思路，我们进一步提出了基于网络结构微扰的链路预测模型（如图7所示）。这个方法在预测丢失的链路以及甄别网络中添加的噪音边两方面都明显超过了经典的层次结构模型和随机分块模型等等。相关算法不仅可以用在社交领域的关系预测中，还可以用在乳腺癌、肺癌、心衰等多种致病基因的预测，预测精度高于传统的系统生物学方法[11]。

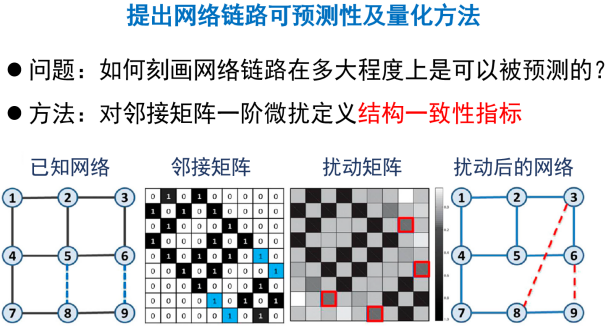
图 7 网络结构一致性计算

网络信息挖掘具有非常广泛的应用场景。目前已有部分研究成果应用于网络舆情监控、致病基因预测、医保欺诈识别、电子商务服务等实际系统中，产生了一定的社会经济价值。二十大报告中强调了产业链供应链对于国家安全的重要性，要求着力提升产业链供应链韧性和安全水平，网络信息挖掘的相关方法也能应用于相关研究中发挥作用。产业链供应链天然就是一张网，可以用复杂网络进行描述刻画（如图8所示），其中供应链是上下游企业为实现将产品或服务交付给最终用户而形成的产-销关系网络，产业链是各产业之间依据一定经济技术联系、空间布局形成的相互关联网络。通过构建网络，就可以通过识别重要节点，提前发现可能被“卡脖子”的产业；通过识别重要链路，优化重要链路及提前预警薄弱环节等，结合从微观节点到宏观网络全局的视角，提出产业链供应链的优化升级策略，保障产业链供应链的自主可控和安全高效。

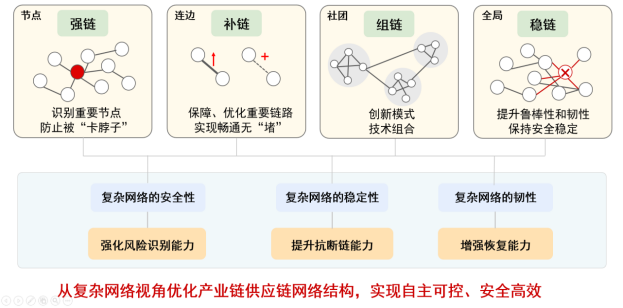
图 8 复杂网络视角优化产业链供应链网络

四、网络科学新前沿——从低阶到高阶

图论作为复杂网络的重要基石之一，其源头最早可以追溯到欧拉的哥尼斯堡七桥问题。直到1998年小世界网络、1999年无标度网络的突破性进展，掀起了网络科学过去二十多年的研究热潮。目前，我们在节点和连边层面对网络的结构、动力学、预测和控制有了较成熟的理解。然而随着研究的不断深入，研究人员发现很多现实系统中不仅包含节点对之间的二元关系，还包括以群、组的形式发生的高阶相互作用[12]，比如，一篇学术论文可能是由多名学者共同完成的；生物信号传递、基因表达调节等生命过程需要多种蛋白质的参与；在大脑神经网络中，包括记忆在内的很多认知功能，都依赖于神经元群的编码和信号同步。这种高阶相互作用难以用基于二元交互关系的网络进行很好地描述。当我们回溯网络科学的起源时，会有一些新的思路（如图9所示）。我们发现，欧拉另外一个重要贡献——欧拉示性数以及庞加莱的洞公式等研究为网络科学提供了新的思路，可以用来研究多节点相互作用的高阶结构和动力学问题，从而将网络科学的研究推进到高阶网络分析的时代。高阶网络分析使我们可以获得对网络的结构和功能更深刻的洞见，并有望在一些已有难题上突破瓶颈、获得新发现。

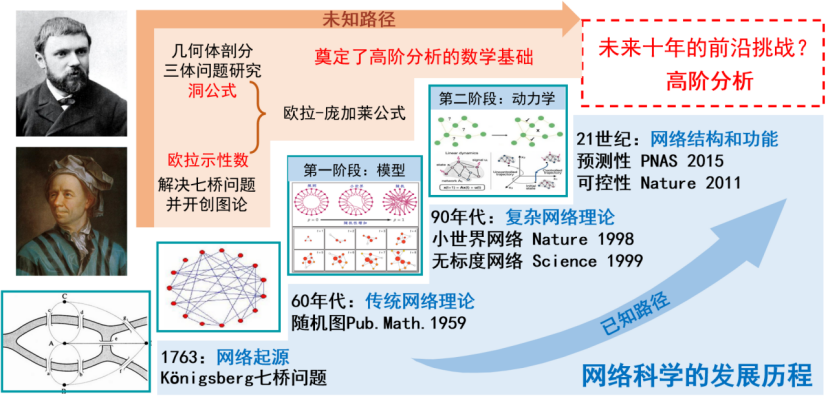
图 9 网络科学发展历程及未来前沿挑战

从社会过程到神经科学的众多复杂系统实例上，高阶拓扑分析都展示出了巨大潜力。网络高阶结构中，最基本的就是圈[ 圈 （Cycle）：一个由相同起点和终点构成的封闭路径。]结构，包括团[ 团 （Clique）：无向图中顶点的子集，一个团中每两个不同的顶点必定相邻。也就是说，其导出子图是完全图。]和洞[ 洞 （Cavity）：网络中圈的无关等价类中的最小圈。]（如图10所示）。而人脑中团和洞，前者作为信息处理和记忆的单元，后者作为跨脑区信息整合和分发的功能基础，对于人脑的并行处理与高级认知活动至关重要[13]。进行网络高阶拓扑分析的首要任务是要找到网络中的高阶结构。但目前为止，关于网络高阶结构的研究还没有形成系统的理论方法。比如绘制大脑完整的高阶结构图谱现在仍是一个巨大的挑战。

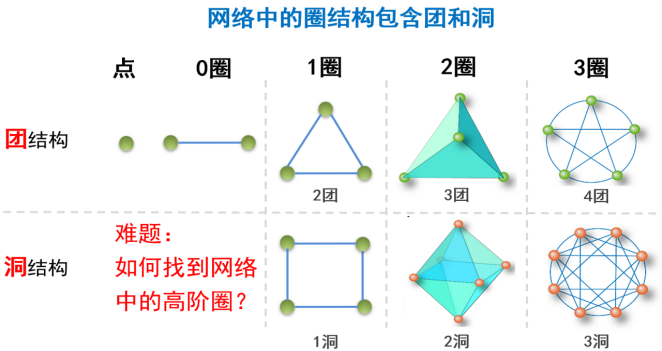
图10 团、洞结构示意图

寻找网络高阶结构的关键在于，如何计算网络结构。我们借鉴庞加莱对几何体剖分的思想，把网络看成一个几何体，然后对它进行类似的剖分，分解成全齐性子网络[14]。然后再采用一些二元域上的向量空间和边界算子对网络进行描述和计算。基于此，我们就可以计算出网络中的团、洞结构，以及拓扑不变量，最后呼应欧拉-庞加莱公式，进一步验证计算的准确度（如图11所示）。我们将这套方法应用在线虫的神经网络中，计算出线虫神经网络全部团、洞的数目，绘制了线虫神经网络完整的高阶结构图谱[15]。而这些团、洞结构的生物学意义还有待进一步解读。

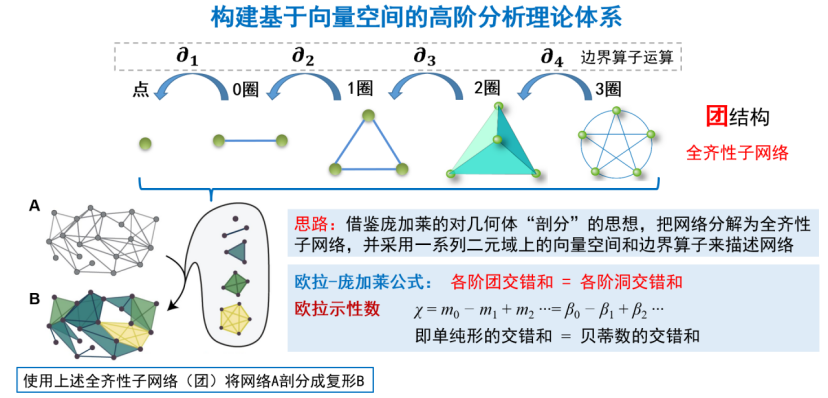
图11 高阶网络分析理论框架

应用高阶网络分析来理解大脑会是一个全新的视角。团、洞等高阶结构在大脑中非常关键，这也将促进我们对脑功能相关的神经环路的理解和认识，为临床应用和开发类脑计算框架提供了新思路。比如，我们对孤独症患者大脑神经网络的分析显示，与健康人相比，孤独症患者脑网络中的“团少洞多”。团在一定程度上反映了局部并行处理信息的能力，洞反映了大脑对不同脑区信息整合的能力。这就说明孤独症患者局部并行处理信息的能力有所降低，但是跨脑区信息整合的能力得到提升。但是具体而言，这些团、洞结构如何以特定的组织方式形成，它们与认知和疾病之间究竟有何关联？这都是未来需要进一步研究的重要问题。

在未来，网络科学与人工智能的结合将有着巨大潜力。它不仅有望解决当前的挑战，比如说现代数字化社会的安全和治理问题，同时也将催生一些新的科学问题和应用技术，在社会、经济等众多领域发挥重要作用（如图12所示）。从1984年圣塔菲研究所成立、复杂性科学诞生，到2021年诺贝尔物理学奖授予复杂系统研究，复杂科学在短短几十年里迅速成长，但它仍然像一个青春期的孩子，既稚嫩又代表着未来。复杂科学方兴未艾，中国学者未来可期！

图12 网络科学与人工智能结合的应用场景

参考文献

[1] 乔治·帕里西. 随椋鸟飞行. 文铮, 译. 2022.

[2] NEWMAN M E J. The structure and function of complex network. SIAM Review, 2003, 45(2): 167-256.

[3] Lü, L., Chen, D., Ren, X. L., Zhang, Q. M., Zhang, Y. C., & Zhou, T. Vital nodes identification in complex networks. Physics Reports 650, 1–63 (2016).

[4] 吕琳瑗, 周涛. 链路预测. 高等教育出版社, 2013[2023-08-12].

[5] Alvarez-Hamelin, J. I., Dall’Asta, L., Barrat, A. & Vespignani, A. k-core decomposition: a tool for the visualization of large scale networks. Preprint at https://doi.org/10.48550/arXiv.cs/0504107 (2005).

[6] Lü, L., Zhou, T., Zhang, Q.-M. & Stanley, H. E. The H-index of a network node and its relation to degree and coreness. Nature Communications 7, 10168 (2016).

[7] Ye, Y., Xu, S., Mariani, M. S. & Lü, L. Forecasting countries’ gross domestic product from patent data. Chaos, Solitons & Fractals 160, 112234 (2022).

[8] Wang, H., Wu, H.-J., Liu, Y.-Y. & Lü, L. Higher-order interaction of brain microstructural and functional connectome. Preprint at https://www.biorxiv.org/content/10.1101/2021.11.11.467196v1.abstract (2021).

[9] 范天龙, 朱燕燕, 吴蕾蕾, 等. DHC定理在有向含权网络上的推广及应用 电子科技大学学报, 2017, 46(5): 766-776.

[10] Lü, L., Pan, L., Zhou, T., Zhang, Y.-C. & Stanley, H. E. Toward link predictability of complex networks. Proceedings of the National Academy of Sciences 112, 2325–2330 (2015).

[11] Zeng, X., Liu, L., Lü, L. & Zou, Q. Prediction of potential disease-associated microRNAs using structural perturbation method. Bioinformatics 34, 2425–2432 (2018).

[12] Boccaletti, S., De Lellis, P., del Genio, C. I., Alfaro-Bittner, K., Criado, R., Jalan, S., & Romance, M. The structure and dynamics of networks with higher order interactions. Physics Reports, 1018, 1-64 (2023).

[13] Sizemore, A. E., Giusti, C., Kahn, A., Vettel, J. M., Betzel, R. F., & Bassett, D. S. Cliques and cavities in the human connectome. Journal of Computational Neuroscience, 44, 115-145 (2018).
[14] Shi, D., Lü, L. & Chen, G. Totally homogeneous networks. National Science Review 6, 962–969 (2019).

[15] Liu, B., Yang, R., Wang, H. & Lü, L. Complete cavity map of the C. elegans connectome. Preprint at http://arxiv.org/abs/2212.03660 (2022).

来源: 自动化学报

内容资源由项目单位提供