人工智能：“肤浅”的统计与深刻的洞察

要清晰完整地理解一个事物，不止要知道它“是什么”，还要知道它“不是什么”，否则就可能在不自觉中夸大了它真实的价值。任何事物都是在与其它事物的联系中“定义”着自己是什么与不是什么。所以要在对比中才能最终形成清晰完整的理解。

那么人工智能中大量运用的统计方法是什么？它是通过对数据做逻辑数值计算处理，来发现这些数据所代表的对象的某些特征性质。

从这个描述中，我们可以看出正反两个问题。首先，统计方法发现的事物的特征性质，一定是通过对所处理的数据做逻辑数值计算处理的结果来揭示的。在这种情况下，这些特征性质的信息必然以某种形式比较充分地包含在了所处理的数据中；其次，如果事物的某些特征性质的信息，没有被所处理的数据所携带，或不够充分，这时统计方法便无能为力。

“暴力计算”的价值，就在于可以用统计方法把数据中所携带的信息，按照人类的需要更加彻底地“压榨”出来。统计方法因“暴力计算”而走向了自己的巅峰。也引发了人们极大的期待。那么是否存在不能够用统计方法发现的特征与性质？答案显然是肯定的。这些特征性质的发现需要统计之外的其它方法或能力。从它们的对比之中，我们或许可以更清楚全面地理解统计方法。人类首先发展起来的科学就是力学。在力学孕育的时代，以伽利略为代表的科学先驱们对物质的运动过做了大量的观察测量。其中第谷·布拉赫（Tycho Brahe，1546年12月14日－1601年10月24日，丹麦天文学家和占星学家）受丹麦国王弗雷德里克二世的邀请在汶岛建造天堡观象台，开始了他持续20多年的对天体运动的详细观测。其观测数据的丰富和精度之高，远非同时代的其他人可比。第谷的测量数据在科学上真正发挥重要的作用，是由开普勒（JohannesKepler，1572年1月6日—1630年11月15日，德国天文学家，数学家与占星学家）完成的。开普勒在1600年慕名将自己在天文领域的研究成果写信寄给第谷。第谷便邀请其做自己的助手。两人一起工作10个月后，第谷意外去世。开普勒因而获得了第谷的所有天文观测数据。他对其中大量的行星观测数据做了深入的统计分析计算，在1602年发现了行星运行的第二定律，在1605年发现了第一定律。这两个定律发表在1609年出版的《新天文学》一书中。然后又经过多年的努力，在1618年他发现了行星运行第三定律并随后发表在1619年出版的《宇宙的和谐》一书中。从数据中分析总结这三个定律前后总共花了近18年的时间。开普勒的行星运行三大定律被称为：轨道定律、面积定律和周期定律。这三大定律可以被分别描述为：所有行星分别是在大小不同的椭圆轨道上运行，太阳位于椭圆的一个焦点上；在同样的时间里行星向径在轨道平面上所扫过的面积相等；行星公转周期的平方与它同太阳距离的立方成正比。开普勒因这三大定律获得了“天空立法者”的称号。这三大定律是典型的数据统计分析的成就。但是数据分析的深度也只能到此为止，只能就这些数据所反映的行星运行状况做规范性的提炼描述。这些统计产生的结果可以“泛化”推广到其它的类似于太阳系这样由一个远远超过其拥有的行星质量的巨大质量星体主宰的星系中，但是对于两个质量相差不大的双星系统，它就失效了。更不要说多个质量相差不大的多星系统以及地面上的自由落体等问题。这三大定律也没有办法告诉我们更深一层的规律：是什么原因让行星以这种方式运行，更没有办法告诉我们行星之外的物体运动规律。这个例子直观地揭示了统计方法的作用与局限：它可以也只能提取和利用统计数据本身所蕴含的事物信息。能够在多大程度上提取和利用这些信息，则取决于所使用的具体的统计方法。一个统计方法核心包括了统计模型以及从数据中提取统计模型参数的算法、即本章图七中上面的“学习算法”这两部分。开普勒是使用了椭圆曲线作为统计模型，本章图五中的火炮位置侦测，则是用抛物线作为统计模型，深度学习用的则是人工神经网络类模型。模型+参数便是用统计方法得到的结果，用于解决与它相匹配的问题。不同的统计方法，其提取和利用不同的信息的能力不一样。选择哪一种统计方法去解决一个具体的问题，是一种如前所述的现代工匠技艺。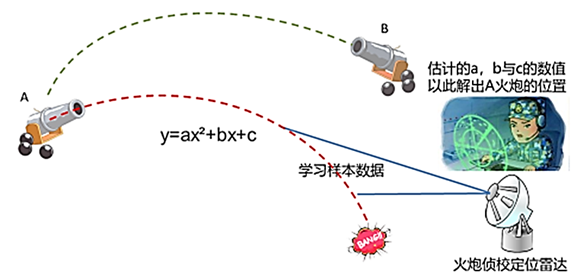

图一 火炮定位的“机器学习”

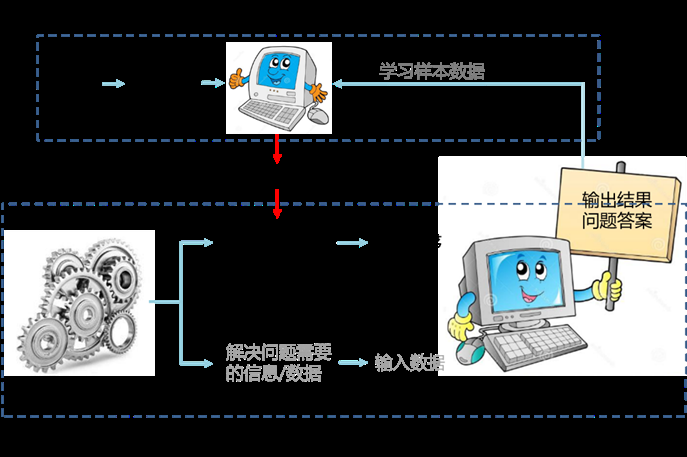
图二 “机器学习”之“在线机器学习”

简而言之，统计方法是一种就事论事的手段。不论是从横向的广度（所谓的泛化）还是从纵向的深度（所谓的本质）上，它都没有办法超出数据自身蕴含的信息所能达到的程度。而“泛化”的能力与对本质的认识又是不可分割的。要想认识更深层的规律，从而获得更好的“泛化”能力，仅仅依靠统计方法的创新是做不到的，它需要不同于数据统计的方法与能力。科学如果仅仅停留在数据统计方法之上，就不会有后来的辉煌了。在超越统计方法这条路上，牛顿做出了里程碑式的巨大贡献。开普勒发表行星运行三大定律多年之后，据说因为一个苹果砸中了牛顿的脑袋而启发了他，让他发现了万有引力定律。在1687年牛顿出版了他的重要著作《自然哲学的数学原理》，其中阐述了万有引力定律与其它三个力学定律。这四个定律具有开天辟地的意义，奠定了人类科学的基础。

图三 苹果砸出了牛顿的灵感

就万有引力定律的发现而言，它固然离不开包括开普勒在内的众多前人的探索成果，一如牛顿所言自己是站在了巨人的肩上。但是它显然不是数据统计分析的直接产物，而是超越了数据所反映的具体事物行为的局限，具有更加一般性的意义。事实上，在《自然哲学的数学原理》中牛顿依据万有引力定律及其它三个力学定律，推导出开普勒行星运行三大定律等一系列的“定理”。而牛顿发明的微积分更是与数据统计无关。

牛顿在《自然哲学的数学原理》一书中提出了多种做科学探索发现的方法，其中与认识本质性普遍规律直接相关的是两个：分析综合与归纳推理。但是它更多的是一种哲学意义上的原则指导，而不是像统计方法那样的具体操作。而且一个人即使知道掌握了分析综合与归纳推理的原则和具体的方法，也未必就能产生对事物本质的认识。自牛顿之后，知晓这些原则的大有人在，但是在科学发展上做出实质性贡献的却屈指可数。

最典型的一个例子便是在前面一章中提到过的洛伦兹与爱因斯坦在狭义相对论上的不同贡献。

1905年爱因斯坦发表了著名的狭义相对论论文《论运动物体的电动力学》。在狭义相对论中，核心的是两个惯性参考系之间，以速度沿轴方向相对运动时的坐标变换：

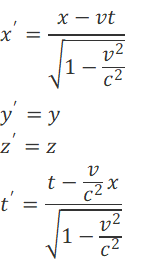
有趣的是这组变换不叫爱因斯坦变换，而是被称为“洛伦兹变换”。这是因为在爱因斯坦的论文发表的前一年左右，荷兰物理学家洛伦兹（H. A. Lorentz，1853—1928，荷兰物理学家，1902年诺贝尔物理学奖获得者）就推导出了这个变换。但不幸的是，他并没有理解这个变换的现实意义，虽然这组变换看上去相当简单，最复杂的数学运算不过是小学就教授过的开平方。形式上的简单，不代表易于理解其蕴含的真实意义。

因为洛伦兹只是推导出了它的数学形式，而爱因斯坦才真正理解了它真实的革命性意义。结果狭义相对论的发明权归了爱因斯坦，虽然这组变换依然冠以洛伦兹的名字。所以杨振宁于2005年7月24日在第22届国际科学史大会上说：“洛伦兹有数学，但没有物理学。”（杨振宁，“爱因斯坦的机遇与眼光”，《科学文化评论》第2卷 第4期）我们常常认为数学公式本身代表了一种深刻，其实相对于数学公式背后的真实意义而言，数学公式本身依然是表象。

开普勒定律与牛顿定律都是用简洁的数学语言表达的，但是它们的普适性有巨大的差异，因而所揭示的规律的深度有极大的不同。牛顿的伟大不仅仅在于他找到了万有引力数学形式，更在于他指出了它适用于宇宙中的万物。所以最终不是看是否找到了漂亮的数学公式，而是要看数学公式到底代表了什么样的真实意义。

牛顿与爱因斯坦显然都有洞悉本质的能力，而这个能力不是掌握了分析综合或归纳演绎的原则就可以拥有的。只有具备了这个能力，才能利用分析综合与归纳演绎的手段，透过层层的现象挖掘出事物背后一般性普遍规律或称本质。迄今为止，我们没有办法用逻辑理性的手段来解析这种意识性能力，所以我们权且称之为人类大脑所特有的一种“洞察”能力。

从具体表象到一般性本质的抽象跨越对人类的发展具有决定性的意义，科学就是这种跨越的结晶。它使得我们从就事论事的费心劳神中解放出来，可以以不变的基本原理去应对万变的纷繁复杂的现象，人类文明因此才有了爆炸性发展。

通过前面的分析我们可以清晰地看到，统计方法与洞察不是一回事。我们还没有办法对洞察做严密的逻辑分析，更不要说把它变成一个算法让“外意识”具有这个能力。所以严重依赖数据统计方法的机器学习，远不具备人类的这种“洞察”能力。我们不能指望依赖统计方法的机器学习，可以产生只有洞察才能带来的那种革命性进步。我们不宜用自己的想象或因为心怀期待，就违背客观事实地去夸大统计方法的能力，牵强附会地把统计方法或其它“外意识”产生的一些预料之外的结果演绎为它们“涌现”出了深刻的洞察能力。

当然上面的分析绝不是否定数据统计方法的价值。事实上今天的科学在需要从现象入手做分析的时候，依然依赖统计方法。但它只是科学的入手起点，对本质的洞见才是终点。

来源: 中国科技新闻学会