我经常去自提柜取我网购的东西。自提柜的取件流程如下：买的东西到了后，物流系统会向你的手机发送一个取件码（例如D333EA），然后你到自提柜那里输入取件码，就可以把你买的东西取出来。

这套流程大家都已习以为常，但是有没有人想过这个问题：一个大的自提柜有几百个柜子，如果我根本没买东西却在自提柜前反复试，或者我按取件码时按错了，会不会也可以碰巧打开一个柜子把别人的货物拿走？

图片来源：图虫创意

答案是否定的。为什么呢？我们可以用数学来回答。

如果你能不吃不喝站在自提柜前24天，并且不被人带走

假设一个自提柜有1000个柜子，每个柜子都对应一个长度为6位的取件码。每个取件码只包含数字0~9以及字母A~Z。如果你随机输入取件码，那么你输入多少次，可以打开一个柜子？

这是一道概率题。首先我们知道，自提柜的取件码都是近似随机产生的。因此，6位取件码中，每位取件码的可能性有36种（10个数字+26个字母），那么输入一次取件码的正确概率为1/(36^6)。一次就能打开1000个柜子中的一个的概率为1000/(36^6)。

如果你对这个数字不敏感，那么我们来计算一下，输入多少次才能让你有1/10的概率打开其中一个柜子。这个次数n的计算公式是：

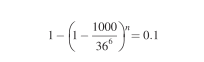
计算得到n≈210720，大概是21万次。假设10秒输入一次取件码，那么你需要不吃不喝地站在那里试超过24天。注意，这还只是1/10的概率。

用数学思维看自提柜的打开概率

如果抛开上面的复杂计算，只用一句话来回答为什么随意试很难打开储物柜，那就是能够打开柜子的取件码，分布得太稀疏了。解释一下分布稀疏的含义。假设你面前有一些柜子，每个柜子都有各自的取件码，并且取件码是在给定范围内随机产生的。

为了让读者们了解得更清楚，现在我们看最简单的情况，假设只有10个柜子，取件码只有1位。那么取件码必然在那10个数字以及26个字母之中。我们可以想象一条直线，这条直线上有36个点（见图6-1），每个点对应一个数字或字母。那么能打开这10个柜子的取件码（在图中为10个大圆点）就是这条直线上36个点中的10个。

从图6-1中可以看出，随意选一个点是容易选中某个大圆点的。这也意味着，比较容易出现随意试一个取件码就可以打开某个柜子的情况。

假设取件码有2位，我们把第一位取件码视为包含36个点的横轴，第二位取件码视为包含36个点的纵轴。因此所有可能出现的取件码就都位于一个二维平面的交叉点上，如图6-2a所示。图中也显示了随机生成的10个能够打开柜子的取件码对应的大圆点。我们可以看出，此时，这10个点的分布十分稀疏。如果随意试很难选中大圆点的位置。

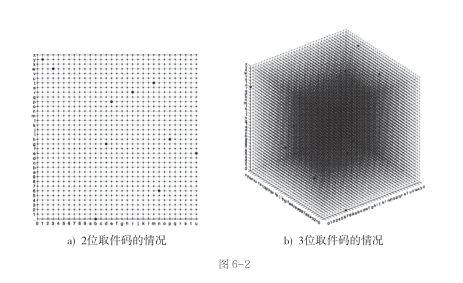
如果取件码变成 3 位，那么取件码就表现为三维空间的点。我们把所有可能出现的取件码对应的点，以及随机生成的10个能够打开柜子的点（大圆点）显示在图6-2b中。可以看出，这10个点变得更稀疏了。

我们可以想象，因为真实的取件码有6位，所以每个取件码都是六维空间中的一个点，能够打开提取柜的取件码的点，会分布得十分稀疏。猜取件码就好像大海捞针，几乎不可能靠运气做到。因此，稀疏性才是取件码具有安全性的关键。

数学思维告诉我们，世界是稀疏的

数学领域对“稀疏性”有明确的定义，如果一个时间信号是稀疏的，那么这个时间信号大部分位置的值都是零。图6-3a显示了这样一个稀疏的时间信号。

如果一个图像是稀疏的，那么这个图像的大部分像素值都是零（对应的颜色是黑色），图6-3b显示了一个稀疏的图像。

我们来看一个现实中的时间信号：

现在智能手环普及度很高，它可以测量人们的运动情况，如图6-4a所示。智能手环用加速度传感器来收集人运动时手臂的加速度的原始信号，再处理信号并得到相应信息，包括走的步数、跑步的距离等。如果我们把加速度的原始信号显示出来，那么其应该类似于图6-4b。

这个加速度的原始信号看起来和图6-3a完全不同，也并不稀疏。

然而，我要告诉你的是，虽然这个加速度的原始信号看起来并不稀疏，但如果用傅里叶级数的方式来表达，它就是稀疏的。（见图6-6）。

我们可以看出，在用来表示原始信号的所有正弦波中，只有少数几个正弦波的频率显得高一点，其他正弦波的频率都非常低。这意味着除了少数正弦波，大部分的正弦波前面的系数几乎等于零。

也就是说，这个时间信号的频域表示是稀疏的。

除时间信号之外，我们日常生活中的图像其实也是稀疏的。其原理和智能手环很类似，虽然图6-8中的原始图像并不稀疏，但是我们可以借助一个在数学上被称为奇异值分解的数学工具，将这个图像拆解成为一系列非常简单的图像的叠加。等式右边的这些图像非常简单，如果仔细看一下，就可以发现这些简单图像都由横条和竖杠组成，但是不同的简单图像中，横条和竖杠的位置不同。

我们可以说，每一个简单图像，都对应了原始图像中的一种模式。

虽然原始图像看起来很丰富，也不稀疏，但是我们可以只用少数的简单图像表示它。

可能有人会说，这样表示有什么好处呢？好处主要体现在数据压缩方面。

简单图像所需要的存储空间比原始图像小得多。通过这种方法，我们只需要把少量比较大的系数对应的简单图像和对应的系数一起存起来，就可以恢复原始图像。这大大压缩了存储需要的空间。

所以你看，数学思维在我们日常生活中随处可见，稀疏就存在于我们所走的每一步路、所存储的每一张图像、所输入的每一个取件码里。很多看起来复杂的现象，背后所包含的规律其实是稀疏而简单的，只要你学会用数学思维。

文章由科普中国-星空计划（创作培育）出品，转载请注明来源。

作者：北京航空航天大学副教授、博士生导师 刘雪峰

审核：华中师范大学数学与统计学学院 副教授 邓清泉

来源: 星空计划

内容资源由项目单位提供