图文详情

开篇提问：在地球上，手中的玻璃杯失手后会掉落到地板上，这是由于玻璃杯与地球之间相互吸引的万有引力作用？还是地球对玻璃杯的重力作用？

今天我们就一起来聊聊时时刻刻影响我们生命与生活的这股力量到底是啥？

什么是万有引力？

说到万有引力，就不得不把牛顿大神搬出来了。

万有引力，全称为“万有引力定律”，为物体间相互作用的一条定律，这是一种先通过现象观察领悟想象出来，然后再通过测量计算验证的物体间的相互作用力，是1687年为牛顿所发现。

牛顿在《自然哲学的数学原理》一书中首先提出，”任何两个物体之间都有一种相互吸引的力，这个力的大小与各个物体的质量成正比例，而与它们之间的距离的平方成反比。”

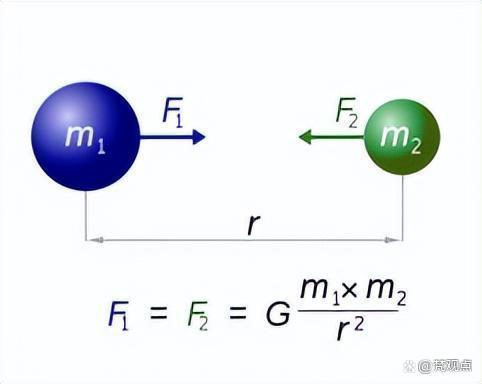
如果用m1、m2表示两个物体的质量，r表示它们间的距离，则物体间相互吸引力为F=（Gm1m2）/r²，G称为万有引力常数也可简称为引力常数。牛顿认为公式中的引力常数G是普适常数，不受物体的形状、大小、地点和温度等因素。

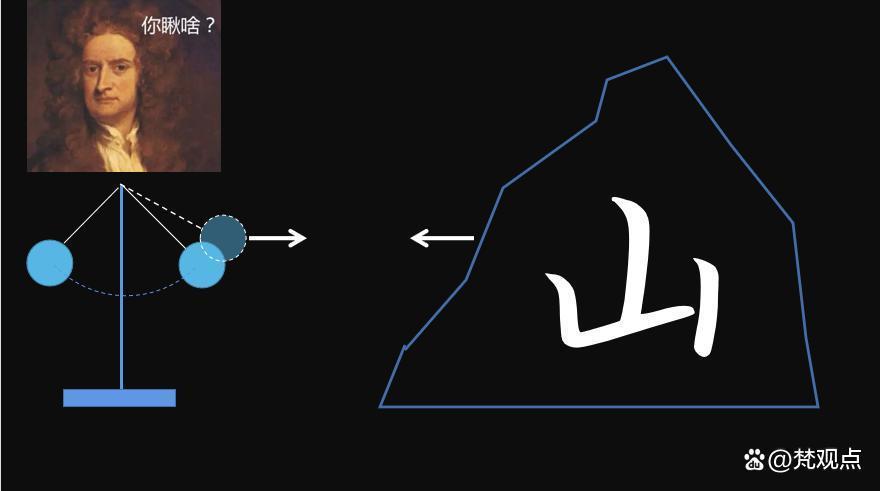
本来牛顿打算测一下这个G的大小，在《自然哲学的数学原理》一书中，牛顿设想了一种可能的计算方式：将一个摆球设置在一座山的附近，由于山会对摆球施加万有引力，所以当摆球运动时，其靠近山的一侧会有微小的偏角，而这个偏角是可以测量的。再由此推算地球的平均密度和质量，最终计算出引力常数。但当时的牛顿认为山对摆的影响是小到无法测量的，最终没有进行实验。这也导致他无法通过测定引力的办法来计算地球的质量。

卡文迪许扭秤

1797年夏，英国物理学家卡文迪许，着手改进米歇尔的扭秤并开始实验。

卡文迪许

1798年，卡文迪许利用扭秤，成功地测出了引力常量的数值，通过大小铅球之间的相互吸引，证明了万有引力定律和万有引力现象。

卡文迪许扭秤

卡文迪许解决问题的思路是，将不易观察的微小变化量，转化为容易观察的显著变化量，再根据显著变化量与微小量的关系算出微小的变化量。

卡文迪许使用扭秤装置测出的引力常数G其值约为6.67×10^-11 N·m²/kg²。之所以使用铅球，是因为万有引力大小与质量有关，铅球可以在较小的体积下创造较大的引力而被观察到。

万有引力定律出现后，才正式把研究天体的运动建立在力学理论的基础上，从而创立了天体力学。简单的说，质量越大的东西产生的引力越大,这个力与两个物体的质量均成正比，与两个物体间的距离平方成反比。地球的质量产生的引力足够把地球上的东西全部抓牢。

地球和月球之间的万有引力有多大？

根据我们已经知道的数据代入万有引力公式可以算出：

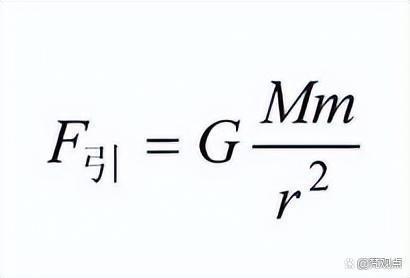
地球和月球之间的万有引力大小=常数*地球质量*月球质量/地球月球之间距离的平方=6.67×10^(−11) m3⋅kg−1⋅s−2 ×5.97×10^24 kg×7.342×10^22 kg/（384399×1000m）^2=1.98×10^20牛顿。根据1牛顿力=1/9.8千克,1千克=9.8牛(顿)，可以换算出约等于2亿亿吨（而地球约有60万亿亿吨）。

人和人之间的万有引力呢？两个质量都是60千克的人，相距0.5米，他们之间的万有引力还不足百万分之一牛顿，而一只蚂蚁拖动细草梗的力竟是这个引力的1000倍！当然如果两个人靠近一点，再靠近一点，两人之间的万有引力的确会增大一丢丢是可能的。

根据万有引力定律，同样一枚硬币面前，同样距离下，体重大的人更吸金。越靠近硬币越吸金。（由此证明笔者我是一个喜欢科普的俗人）

在物理学上，万有引力表示的是物体之间加速靠近的趋势。万有引力是自然界的四大基本相互作用之一，另外三种相互作用分别是电磁相互作用、弱相互作用及强相互作用。万有引力是上述相互作用中作用力最微弱的，但是在超距上万有引力仍然具有较强的主导作用。

以太阳系来举例：太阳与地球间有万有引力作用，太阳与月亮间也有，地球与木星间有万有引力作用，与木星的卫星木卫一也有相互作用，而木星的木卫一与遥远的天王星仍然有相互吸引的作用。这些作用力看似挺复杂，但是太阳系目前所有天体之所以按现在的方式在运行，都是各种万有引力加减乘除之后的合力的最终大小效果决定的。

什么是重力？

这里先纠正一个观念，重力不是牛顿发现和定义的。在牛顿定义万有引力之前的17世纪早期，人们已经能够区分很多力，比如摩擦力、重力、空气阻力、和人力等。牛顿首次将其中一些看似不同的力准确地归结到万有引力概念里：比如物体下落，人有体重，月亮围绕地球转，所有这些现象都是由万有引力引起的。

而其实在很早以前的我们中国古代，就有一个人隐晦地指出了重力的存在。这个人就是老子。

老子在《道德经》中讲“上善若水”，最高的善是像水那样。水有七种善，其中第一个善是“居善地”。那么什么是善地呢？水总是向低处流，喜欢居于低洼的地方，所以，低洼的地方就是善地。而水喜欢往低处流的这种性，就是地球对水的重力作用。

重力与万有引力的区别

重力可以理解为地球阻碍地表附近物体发生移动的一种阻力，它是万有引力的一个分力。重力的施力物体是地球。

重力的方向总是竖直于物体终止位移的最终平面。但不一定是指向地心的（只有在赤道和两极指向地心）。物体受到的重力的大小跟物体的质量成正比，计算公式是：G=mg，g为比例系数（称为重力加速度），大小约为9.8N/kg，重力并不一定等于万有引力，重力随物体所在位置的纬度大小而改变，质量为1kg的物体受到的重力为9.8N。重力作用在物体上的作用点叫重心。

由于地球本身的自转，除了两极以外，地面上其他地点的物体，都随着地球一起，围绕地轴做近似匀速圆周运动，这就需要有垂直指向地轴的向心力，这个向心力只能由地球对物体的引力来提供，我们可以把地球对物体的引力分解为两个分力，一个分力F向，方向指向地轴，大小等于物体绕地轴做近似匀速圆周运动所需的向心力；

向心力的大小在两极为零，随纬度减少而增加，在赤道地区向心力大小达到最大。但是即便这样，物体的向心力还是很小的，所以在一般情况下，可以近似认为物体的重力大小等于万有引力的大小。

物体的重力大小只取决于物体的质量，即物体所包含物质的多少，以及当地的重力加速度决定的。重力加速度g与物体所处的纬度和高度有关：

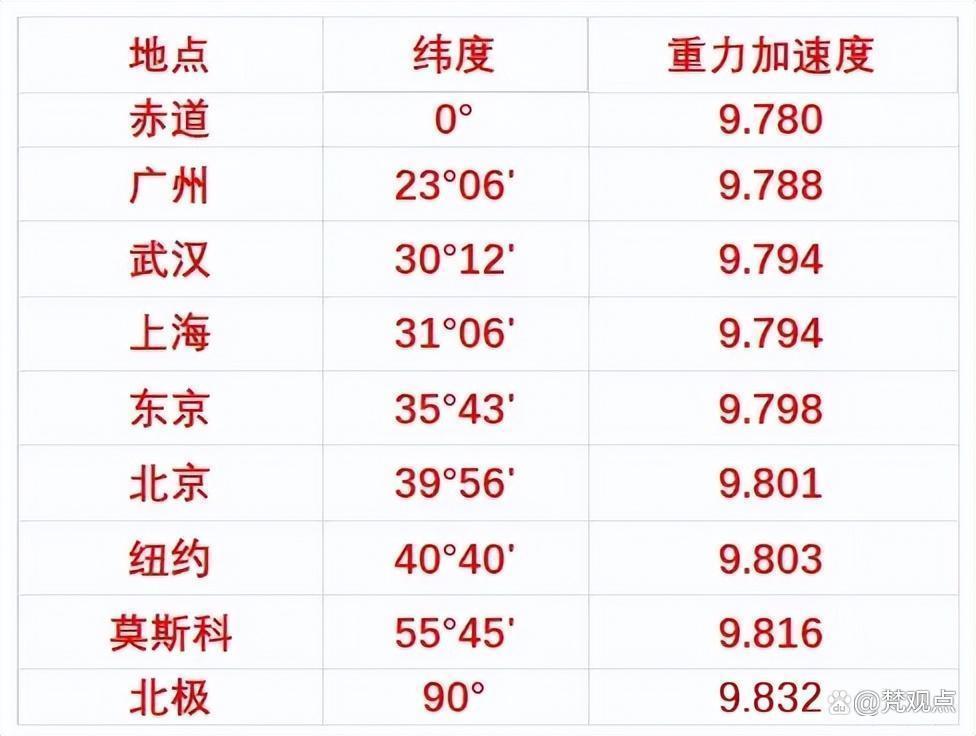
g随纬度的升高而增大，在赤道处g最小，在两极处g最大；

在同一地点g随高度的升高而减小。

所以在地表时重力只是万有引力的一个分量。

但如果我们离开地表呢？比如天空中飞行的飞机？或者太空中的卫星呢？

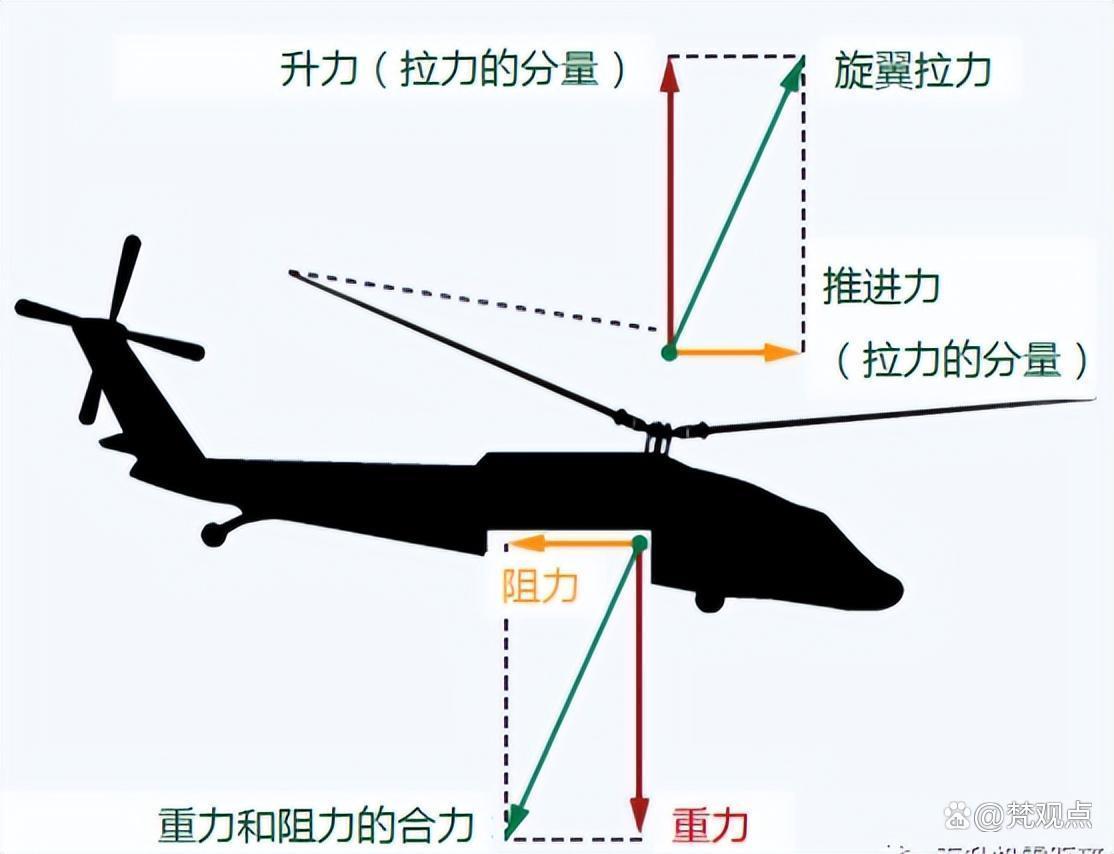
在天空中飞行的飞机，万有引力的重力分量用于客服机翼产生的升力和空气产生的阻力。飞机受到的重力是mg,m是飞机质量,g是重力加速度。所以飞机飞得越高其受到的重力越小，而万有引力的向心力分量也相应变化，速度越快需要越大的向心力。

而对于绕地球做圆周运动的物体（如卫星），我们可以说它是几乎完全失重状态，因为这个时候地球对于卫星的万有引力几乎全部用于提供该物体围绕地球做圆周运动而不跑掉所需的向心力。也可以说此时的重力就是万有引力而对抗了离心力。

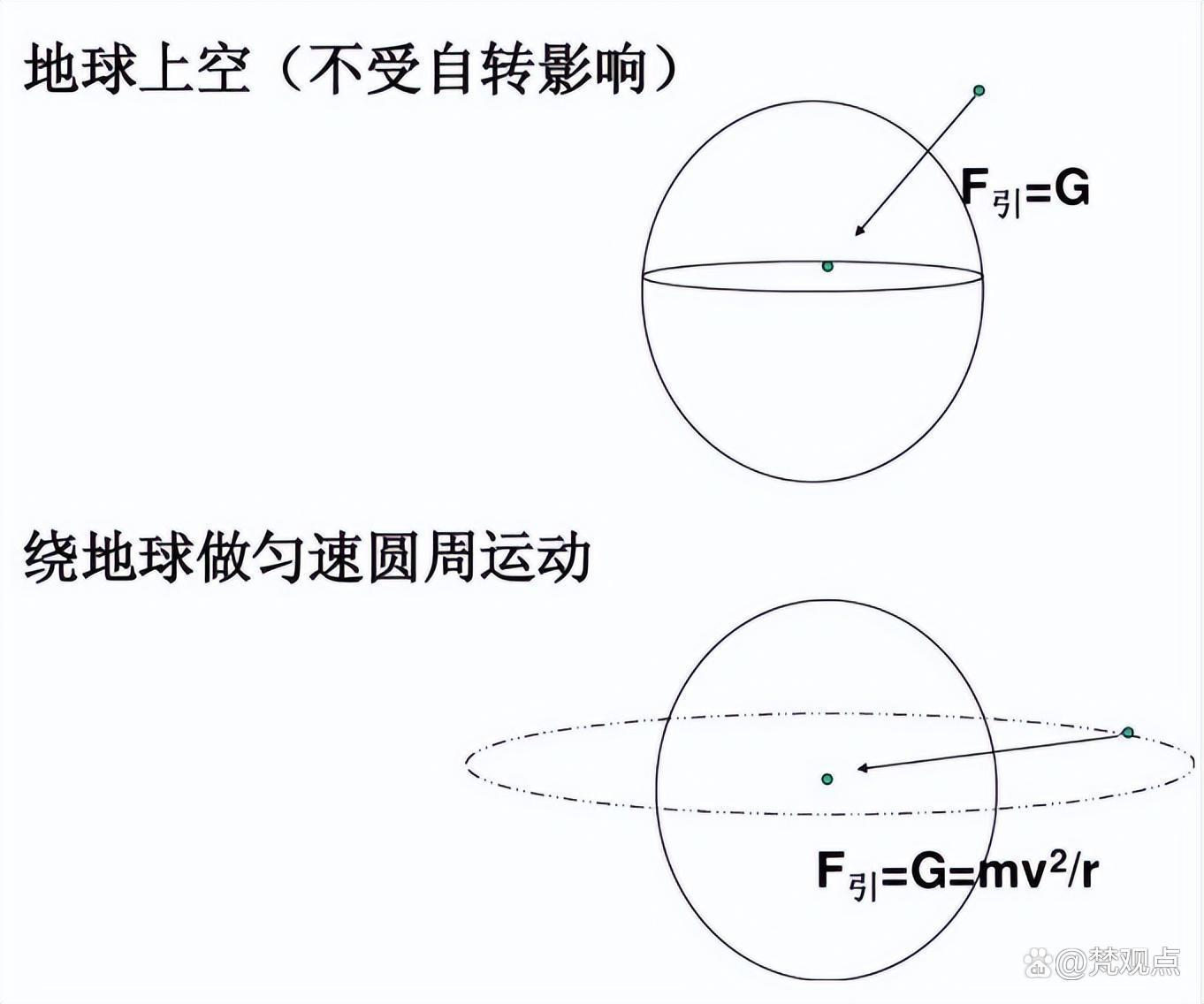
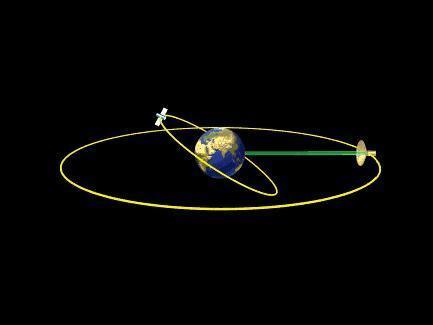
不过其实卫星，尤其低轨道卫星的受力会更复杂一些，下面这些力对卫星都会有影响。

非中心引力

日月引力

太阳辐射光压

地球潮汐作用力

高层大气阻力

而假设在宇宙深空中，由于没有距离某一个天体非常的近，所以可以认为，一个物体受到来自宇宙所有物体的万有引力，但是这些力的合力为0，最终就表现出不受力状态。

地球重力场地球对表面物体具有吸引力，重力加速度是度量地球重力大小的物理量。按照万有引力定律，地球各处的重力加速度应该相等。但是由于地球的自转和地球形状的不规则，造成各处的重力加速度有所差异，与海拔高度、纬度以及地壳成分、地幔深度密切相关。

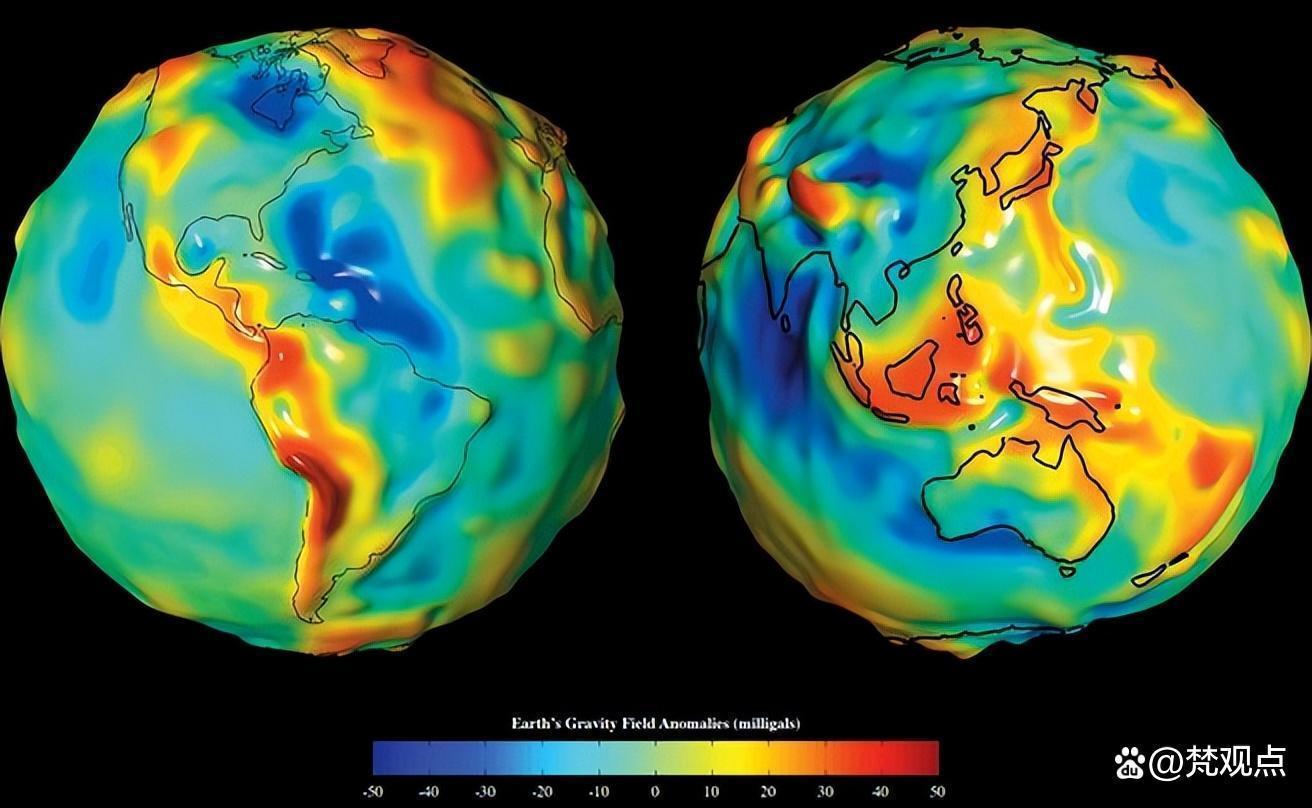
十年以前，欧洲空间局（European Space Agency，ESA）发射了一颗最具创新性的卫星：地球重力场和海洋环流探索者（Gravity field and steady-state Ocean Circulation Explorer，GOCE）。GOCE用了四年的时间，测量自然界的一个基本作用力——万有引力。