下文编译自旧金山大学数学名誉教授 John Stillwell 为其新书 The Story of Proof: Logic and the History of Mathematics 撰写的导读文章,他在文中通过毕达哥拉斯定理展示了“证明”的意义——“证明”是用任何人都能理解的陈述,来让我们相信本来不相信的东西。
The Story of Proof 讲述了一个生动的故事:数学如何发展新的概念和想法,以解决难题。对于任何对当代数学及其发展方式感兴趣的人,这本书都将非常有价值。
撰文 | John Stillwell(旧金山大学数学名誉教授)
翻译 | 下雪
在许多年前的一堂数学入门课上,一个学生问我:“为什么你要证明一切;为什么不直接告知我们呢?”从那以后,我一直在思考这个问题。理查德·戴德金(Richard Dedekind)在其1872年的著作中给出了简短而明智的答案,该书的英译本是 The Nature and Meaning of Numbers 。
在科学中,任何可以证明而没有证明的事情均不应被接受。下面这段关于17世纪哲学家托马斯·霍布斯(Thomas Hobbes)的轶事,可以更好地解释证明是如何起作用的,摘自约翰·奥布里(John Aubrey)有趣而古怪的故事集 Brief Lives。> 他在40岁的时候才开始研究几何学,而这始于一次偶然。在一位绅士的图书馆,欧几里得的《几何原本》摊开在桌面上,正好是命题47。他读了这个命题。通过G……,他说这是不可能的!(他有时会以强调的方式郑重宣誓)于是他读了证明,这促使他回到了他读过的一个命题。而那个命题再次促使他去找另一个他读过的命题。就这样,他最终以证明的方式确信了那条真理。这也让他爱上了几何学。
Brief Lives
因此,数学上的证明就是能让霍布斯相信最初他认为不可能的事情,通过每个人都可以接受的陈述——现在被称为公理——达到最终的结果。这就是公理化方法,在公元前300年左右,它由欧几里得的《几何原本》首次给出,而现在所有数学家都在使用它。
现在,我必须告诉大家令霍布斯震撼的“命题47”就是毕达哥拉斯定理(即勾股定理),现在高中生都很熟悉它。事实上,早在毕达哥拉斯(和欧几里得)之前,它就已被一些古老文明所理解了。大部分人都知道,这条定理是说:直角三角形中,斜边长度的平方等于另外两条边长度的平方之和。例如,在下图中,灰色正方形的面积等于两个黑色正方形的面积之和。

乍一看,这个等式难以置信——也难怪霍布斯不相信,但有一个非常聪明的方法来让它看起来变得很显然,可能在远古时代人们就已知道了这个方法。注意下面两张图,其中每个大正方形内都包含四个三角形。
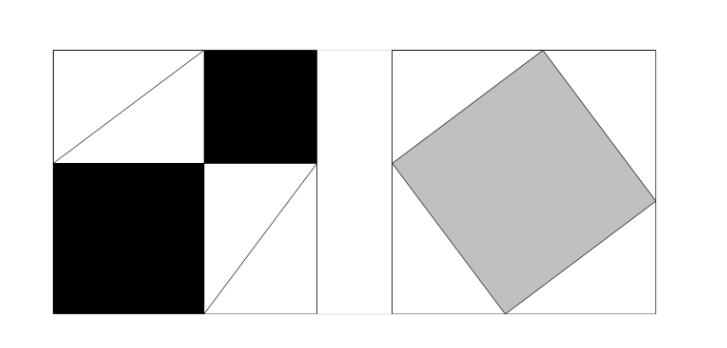
在左图中,我们看到黑色正方形的面积,即三角形两直角边长度的平方和,等于大正方形的面积减去四个三角形的面积。而右图中,大正方形面积减去四个三角形面积等于灰色正方形的面积,也就是斜边长度的平方。
为什么欧几里得要费尽心思来证明它呢?我们相信,答案就在于毕达哥拉斯定理的结论,它使毕达哥拉斯的世界陷入混乱:这就是2的平方根的无理性。
当直角三角形的两条直角边长度都为1时,2的平方根就出现了。在这种条件下,邻接两条直角边的每个正方形面积都是1。根据毕达哥拉斯定理,斜边的平方是1+1=2,因此斜边的长度就是2的平方根,即√2。那么,√2到底是多少呢?毕达哥拉斯学派被这一发现震惊了,尽管他们可以用3/2、7/15、41/29、99/70等非常接近√2的分数近似表示它,但是**没有一个分数恰好等于√2。**这就是为什么我们说√2是无理数,意思是“不能用整数之比表示”,也暗示这是“不合理”的。似乎几何的世界——长度、角度和面积所生活的世界不能与1、2、3、4、5……所生活的的数字世界相协调。这一发现粉碎了毕达哥拉斯学派的世界,他们信奉“万物皆数”。传说这一不受欢迎事实的发现者遭到了惩罚,或者说受到了“神的制裁”——他被扔进了海里。
无论如何,数字和几何之间明显的不可调和,似乎是导致希腊人用不言而喻的公理而非数字推导出几何的原因。这确实很难做到。举个例子,人们必须重新思考正方形(面积)的“和”的意义,以及这个“(面积)和”“等于”另一个正方形的意义。还必须用清晰的语言来表述这一切,以免发生误解。而欧几里得为了克服这些困难而发展的公理化方法一直持续到今天。诚然,《几何原本》中存在一些小漏洞,但公理化方法举世无双,是当今数学研究的典范。现在也有更综合的公理系统,它们成功地统一了几何世界和数的世界。
虽然公理化方法在原则上无懈可击,但实际撰写证明时很容易出现人为的错误。像其他人一样,数学家也会犯错,而在很长的证明中(这在20世纪变得很普遍),错误可能很难被发现。它们往往隐藏在作者跳过的一些冗长或重复的细节中,往往有诸如此类的评注,"这很容易检查"或"这个证明与以前的情况类似"。不过,避免错误是可能的,就像人们避免计算中的错误一样:通过机械化的过程。这可以实现是因为一个完整的证明必须是每个合格的专业读者都能理解的,相当于不用思考就能检查,因此证明可以通过机器检验。证明过程的机械化与计算的机械化基本相同。
遗憾的是,编写机器可检查的证明需要大量的人力,并且他们要对相关数学有深入了解。到目前为止,只有少数真正很长的证明被重写成机器可检查的形式(而由人们撰写的原始证明确实是基本正确的)。在那些等待被改写为可机器检验的形式——甚至是只有数学专家才可以理解的形式而重写的证明中,最著名的例子就是所谓的abc猜想。这个猜想有一些技术性,它与一个简单等式a+b=c中的a、b、c的质因数有关。但该猜想对数论学家来说很有意义,因为它会产出许多引人注目的结果。
自2012年以来,一小群数学家发表了他们所确信的abc猜想的证明。这个“证明”未能说服其他大多数数论专家,他们指出“证明”中似乎有一个漏洞。这两个群体之间的争论已经持续了10年之久,我称之为(为了避免提及名字)abc-信徒和abc-怀疑者。原则上,他们的争议可以通过将“证明”转换为机器可检查的形式来解决。但是abc-信徒声称这是不必要的,唯一的问题是abc-怀疑者的“无知”。
最近几个月,当abc信徒转向数学史时,这个本已奇怪的争论变得更加奇怪了。他们把自己比作不幸的、被迫害的毕达哥拉斯主义者,因为他们发现了无理数√2。他们警告说,如果abc-怀疑者占了上风,将会有“可怕的后果”。
好吧,我们拭目以待。但历史告诉我们,如果abc信徒想模仿欧几里得,重建数学以适应他们的思想,他们必须首先用一种人人都能理解的语言来写作。
希望不会出现如下场景(Sdiney Harris 的漫画):


书籍介绍

通过数学史上的关键事件,本书研究了“证明”(proof)概念的演变。从毕达哥拉斯定理一直到现代,旧金山大学教授 John Stillwell 认为,“证明”思维激发了数学创新活力,并在知识生产方面发挥了关键作用。
作者从欧几里德和他对几何学发展及证明方法的影响开始,谈论到后来的代数与几何学。Stillwell 着手研究数论、非欧几里得几何学、拓扑学和逻辑学等领域,并探究自然数算术和实数之间的深层鸿沟。其中,康托尔、哥德尔、图灵等人发现,证明的概念最终构成了算术的一部分。这一惊人的事实对哪些定理可以被证明、哪些问题可以被解决施加了根本限制。
名家推荐
“这本书完全可以作为一部数学史。......[Stillwell] 在收集和归类这一领域的许多最重要的思想方面做得很好。”——Jim Stein, 《数学新书》(New Books in Mathematics)
“我非常欣赏 Stillwell 的写作,这本书也没有让我失望。他在数学史上具有广泛而权威的影响,能把读者带入那些具有创新性,并发挥关键作用的地方。”——David M. Bressoud,Calculus Reordered: A History of the Big Ideas 的作者
“这是一个生动的故事,讲述了数学如何发展新的概念和思想,以解决棘手的问题。对于任何感兴趣当代数学及其形成的人来说,这本书都是非常有价值的。”——Jeremy Avigad,卡内基梅隆大学
“The Story of Proof——一本关于作为证明的数学,和作为数学的证明的书,历久弥新,令人赏心悦目。”——Anil Nerode,康奈尔大学
本文由“返朴”翻译,首发“普林斯顿读书汇”。
本文受科普中国·星空计划项目扶持
出品:中国科协科普部
监制:中国科学技术出版社有限公司、北京中科星河文化传媒有限公司

来源: 返朴


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助
 返朴
返朴 
