在《三体》的第一部中，作者描写在虚拟游戏中牛顿和冯.诺伊曼拜访秦始皇，说服秦王用三千万秦兵组成人列计算机。历史上冯.诺伊曼发明了奠定现代计算机基础的冯.诺伊曼体系，在小说中，作者利用冯.诺伊曼向秦始皇介绍他的计划巧妙地科普了一些计算机原理，只不过构成计算机的不是半导体或晶体管，而是纪律严明的大秦士兵。

值得一提的是，这个情节在刘慈欣以前的短篇科幻小说《荆轲刺秦王》出现过，在《荆轲刺秦王》中，是荆轲而不是冯.诺伊曼向秦王推销他的计划。

那么，小说中的这个人列计算机是怎么回事呢？请看下面这段：

秦始皇挥手召来了三名士兵，他们都很年轻，与秦国的其他士兵一样，一举一动像听从命令的机器。

"我不知道你们的名字，"冯•诺伊曼拍拍前两个士兵的肩，"你们两个负责信号输入，就叫‘入1’、‘入2’吧，"他又指指最后一名士兵，"你，负责信号输出，就叫 ‘出’吧，”他伸手拨动三名士兵，"这样，站成一个三角形，出是顶端，入l和入2是底边，"

"哼，你让他们成楔形攻击队形不就行了?"秦始皇轻蔑地看着冯•诺伊曼。

牛顿不知从什么地方掏出六面小旗，三白三黑，冯•诺伊曼接过来分给三名士兵，每人一白一黑，说:

白色代表0，黑色代表1。好，现在听我说，出，你转身着着入1和入2，如果他们都举黑旗，你就举黑旗，其他的情况你都举白旗，这种情况有三种:入1白，入2黑;入1黑，入2白;入1、入2都是白。"

"我觉得你应该换个颜色，白旗代表投降。"秦始皇说。

兴奋中的冯•诺伊曼没有理睬皇帝，对三名士兵大声命令:"现在开始运行!入1入2，你们每人随意举旗，好，举!好，再举!举!"

入1和入2同时举了三次旗，第一次是黑黑，第二次是白黑，第三次是黑白。出都进行了正确反应，分别举起了一次黑和两次白。

"很好，运行正确，陛下，您的士兵很聪明!"

“这事儿傻瓜都会，你能告诉朕，他们在干什么吗?"秦始皇一脸困惑地问。

"这三个人组成了一个计算系统的部件，是门部件的一种，叫‘与门'。"冯•诺伊曼说完停了一会儿，好让皇帝理解。

冯所介绍的，是计算机的基本构件——‘与门’，在文中加粗的那一段，描述了与门的特点：当两个输入都为1时，输出为1，其余情况输出为0。用符号表示如下：

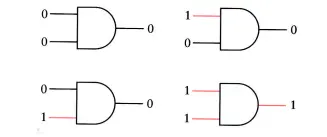
与门

而除了与门以外，还有或门，和非门，冯也用相似的手段，利用大秦士兵组成，他们用符号分别表示为：

或门

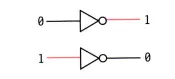
非门

与、或、非，这三种基本逻辑运算是整个计算机的基础。在这三种运算的基础上，我们得以构建出一台精密的计算机。

我们可以想象出来，由三千万大秦士兵组成的一台“计算机”，黑色和白色的棋子此起彼伏，而计算机的运算速度就取决于士兵们的反应速度。

那么我们现实中的计算机是怎样组成的呢？很简单，原理同上，但是那些部件不是人，而是电子元器件，毕竟，电子的速度要比人快多了，同时它还很小。

虽然电子元器件相对于人来说很小，但是世界上第一台电子计算机还是像一间屋子一样大（但是相比于三千万人来说，好多了不是吗）。以我们今天对计算机（电脑）的印象来说很难理解，不仅是因为他的体积，而是它没有显示器，没有键盘，没有鼠标，并且，它能用来干什么？

计算机的功能本质上来说只有一个——计算，而我们今天用电脑做的所有事情，上网，玩游戏，看视频，从本质上来说都是计算机的计算过程，只不过是信息的表示模式不一样罢了。

有了显示器，我们可以更好地阅读计算机计算的结果；有了鼠标和键盘，我们可以更加方便地输入信息和指令。当你在玩游戏时，计算机接受你的键盘的摁键和鼠标的移动所产生的信号，从而计算出你的人物的移动，生命值的变化，通过图像处理以后显示在屏幕上，这一切，都是计算。

现代电子计算机已经无数的更新换代，我们在有了晶体管后由发明了半导体，通过集成电路技术制成的芯片，使得我们的计算机越来越小，操作系统和软件的发展使得功能越来越丰富，但电子计算机结构依然遵循冯.诺伊曼体系。

让我们抛开显示器，键盘，鼠标，半导体，芯片这些现代计算机的标志，我们以最原始的手段实现最简单的计算过程为例，希望可以帮助大家更好地理解计算机。

（参考自《编码：隐匿在计算机软硬件背后的语言》，作者：Charles Petzold)

我们用电路来实现信号的传递，用电路的通和断来表示1和0，相信大家都了解计算机中的信息是以二进制存储的。我们用最简单原始的方法，看下图：

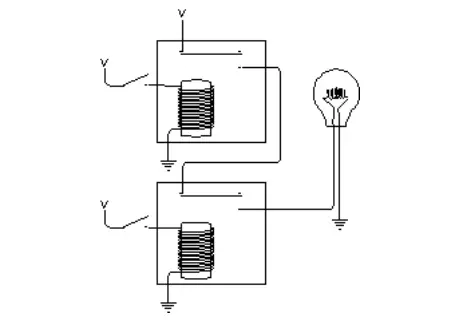
与门

上图是一个电路图，左边连个开关控制着两个继电器，当开关闭合时，继电器通电产生磁力，通过吸引金属片使得连个串联在灯泡电路上的连个开关闭合，灯泡通电发光。

左边两个开关就是我们的“鼠标和键盘”，而灯泡就是“显示器”，他们就是输入和输出设备，我们通过开关的闭合表明我们想输入的是1还是0，而观察灯泡，来阅读计算结果。

在上述电路中，进行的是一个与的运算，只有连个开关同时闭合时，灯泡才会发光。

同理，我们也可以构建或门和非门：

或门

非门

我们现在已经通过原始的手段组建了基本的逻辑运算功能，接下来我们用这三种基本运算实现一个二进制的加法机。

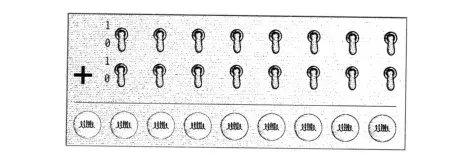
他的控制面板如下，两排开关，可以让我们输入2个八位的二进制形式的加数，而第三排的9个灯泡显示的运算结果。

然我们想一下二进制的加法过程，假如这两个数都只有一位，那么运算过程为：

我们把它分解为连个运算，一种是和运算，一种是关于是否进位的运算：

对于进位运算我们可以发现他就是与门，而和运算似乎不属于三种基本运算，但是我们可以通过基本运算构造出这种运算：

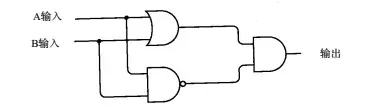
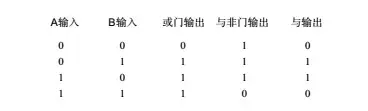
它由2个与门，1个或门和1个非门构成，图中与门上加上一个小圆圈表示在与门的输出位置加上一个非门，组成与非门。

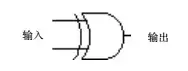
为了方便表示，我们将异或门表示为：

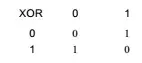
现在，我们将和运算和进位运算组合起来，组成为半加器，并将它符号化：

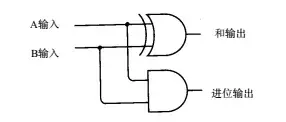
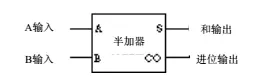
半加器只能计算1位二进制数的加法，为了进行更多位的运算，需要将半加器的进位输出传递给下一位数的运算。在此基础上，我们构建出全加器，并符号化：

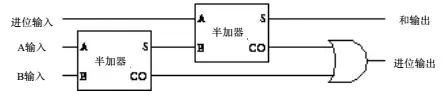
现在我们将这些全加器组装起来，首先是最右边的全加器，由于它是最低位，所以不接受进位输入：

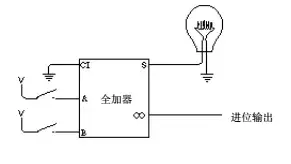
然后从右往左数第2位到第7位的全加器的进位输入连接到比他第一位的全加器的进位输出：

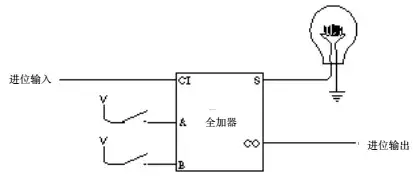
最左边的全加器，他的进位输出连接到另一个灯泡上：

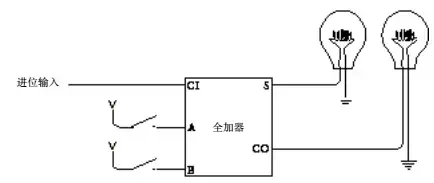
最终，我们的8位二进制加法器就完成了，虽然它的功能很简单，但是这向我们证明了计算机的可行。

现代计算机的功能可远不止这些基础的运算，通过这些与门，或门，非门的组合，我们可以构造出存储器，地址选择器，等等。

遗憾的是，在这里我们无法将其介绍清楚，因为他们比加法运算更加复杂。

感兴趣的同学可以去看Charles Petzold的著作《编码：隐匿在计算机软硬件背后的语言》，上文中以电子元器件构造加法机的这一令人兴奋的想法便来自此书。

理论上，我们完全可以用这种凡是制造出一台计算机，事实上，早期的电子计算机就是用继电器组成的，这也是它的体形如此巨大的原因，他的输出就是一排排的指示灯。同时以继电器构造计算机也会导致计算机的运算速度受到限制，因为如果金属片开关的摆动速度影响了信号的传递。

我们反观人列计算机这一设想，就会发现它比继电器组成的计算机还要惨，因为人出错的机率要远远大于机器，而且计算机的运行成本（三千万人的吃喝住宿）也过于昂贵。

不过，不管是人列计算机，还是继电器计算机，或者是现代大规模集成电路计算机，他们背后所依据的计算原理都是一样的，其基本构件就是：与门，或门，非门。

来源: 九象科普