概念

对于一个无记忆离散信源中每一个符号，若采用相同长度的不同码字代表相应的符号，就称为等长编码。一般来说，若要实现无失真的编码，这不但要求信源符号与码字是一一对应的，而且要求码符号序列的反变换也是唯一的。也就是说，一个码的任意一串有限长的码符号序列（码字）只能被唯一地翻译成所对应的信源符号序列。

若对一个简单信源S进行等长编码，那么信源S存在唯一可译定长码时必须满足的条件是

其中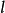 是等长码的码长。例如信源S共有q=4个信源符号，现进行二进制等长编码，其中码符号个数为r=2。信源S存在唯一可译等长码的条件是码长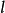必须不小于2。

基本原理如果对信源S的N次扩展进行等长编码，且设信源，有q个符号，那么它的N次扩展信源共有个符号，其中是长度为N的信源符号序列。而设码符号集为是基本码符号集X的个数。当把这些长为N的信源符号序列变换成长度为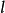的码字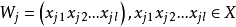时。根据前面的分析，若要求编得的等长码是唯一可译码则必须满足

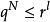
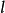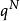此式表明，只有当长的码符号序列数不小于N次扩展信源的符号数时，才可能存在等长非奇异码。

这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。1