定义

余数系统是一种无权的运算，各个模运算之间具有天然的独立、并行特性,相互之间不存在进位。因此，采用余数系统来提高模乘和模逆的运算速度，挖掘模乘和模逆的并行性，在当今密码算法的大运算量时代，对提高公钥密码算法运算速度，具有重要的研究价值。

近年来，用RNS算术设计专用数字处理机的工作越来越多，主要原因之一就是RNS算术内在的模块结构造成的无进位操作，可以存储到ROM中以实现高速计算。模块性提供高速、错误隔离，容易扩充字长，以及容错的性能，这些对VLSI体系结构都是很重要的。1

中国剩余定理余数系统，具有悠久的历史，是以中国余数定理为基础的。

历史背景中国南北朝时期的数学家孙子所著的《孙子算经》中记载“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”是一个古老的命题－－公元420年～589年

后由南宋时期的数学家秦九韶在他的《数书九章》系统地论述了一次同余式组解法的基本原理和一般程序，于12世纪末流传到欧洲，被称为“中国剩余定理”(CRTChineseRemainder Theorem)，这是最早的余数系统(RNS－Residue Number System)。– 秦九韶（约1202至约1261），自称鲁郡（今山东省曲阜一带）人，生於普州安岳（今四川省），南宋数学家、天文学家。

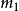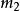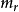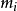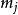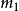
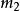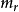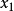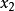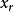定理内容设 ， ，…， 为两两互素的正整数，即gcd( ， )=1,i≠j。M= …， ，并有 ， ，…， 满足下列同余方程组：

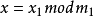
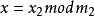
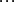
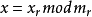则方程组有解，且在mod M的剩余系统中有唯一解。

应用近年来，用余数系统算术设计专用数字处理机的工作越来越多，主要原因之一就是RNS算术内在的模块结构造成的无进位操作，可以存储到ROM中以实现高速计算。借助余数系统进行了许多工作，如下所示：

模加法器和模乘法器设计在余数系统中,模加法器与模乘法器属于最基本也是最重要的算术运算单元,因此提高余数系统中模加法器与模乘法器的性能具有重要意义。2

检测单元与运算单元随着集成电路行业的高速发展,对芯片设计在速度与功耗方面的要求越来越高,采用过去传统的并行技术已经无法满足设计对高性能的要求,因此需要引入诸如余数系统这类真正并行处理的数值表征系统。在余数系统中,其各通道间彼此独立、并行以及免进位传播的特点,可以使得余数系统在高速数字处理领域具有很大的应用价值,因此对余数系统相关问题的研究是非常有意义的。3

FIR滤波器的研究在数字信号处理领域中,有限脉冲响应滤波器（FIR）以其内在的稳定结构成为人们的研究重点。FIR滤波器常常需要在短的时间内，完成大量非零项的多次无损乘加运算，才能保证理想的频率响应指标。然而,传统的二进制数系统下的FIR滤波器在超高速信息流的场合下，难以同时满足实时通信及滤波精度的要求。余数系统以其内在的并行性、模块化以及容错性强的特质为设计高性能的FIR滤波器提供了一个有效的方法。4

OFDM无损峰均比抑制方法正交频分复用(OFDM)传输方法输出信号由多个子信道叠加而成，会产生较高的峰均比。提出一种基于余数系统的峰均比抑制方法，利用余数系统并行、余数小于对应余数基的特性，从信号前端入手控制OFDM传输信号的动态范围，有效利用放大器的线性动态范围,防止非线性失真的产生,达到无损抑制峰均比的目的。5