在数学中，双曲函数是一类与常见的三角函数（也叫圆函数）类似的函数。最基本的双曲函数是双曲正弦函数 sinh 和双曲余弦函数 cosh，从它们可以导出双曲正切函数 tanh 等，其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。

双曲函数的定义域是实数，其自变量的值叫做双曲角。双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。

基本定义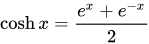

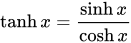
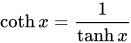
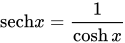
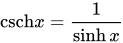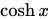函数 是关于y轴对称的偶函数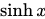。函数 是奇函数。

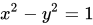
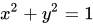如同当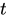 遍历实数集时，点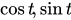（ ）的轨迹是一个圆 一样，当t遍历实数集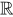时，点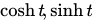（）的轨迹是单位双曲线的右半边。这是因为有以下的恒等式：

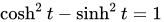参数t不是圆角而是双曲角，它表示在x轴和连接原点和双曲线上的点（的直线之间的面积的两倍。

历史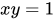 在18世纪，约翰·海因里希·兰伯特引入双曲函数，并计算了双曲几何中双曲三角形的面积。自然对数函数是在直角双曲线下定义的，可构造双曲线直角三角形，底边在线 y=x上，一个顶点是原点，另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数，是自然对数的逆函数指数函数，即要形成指定双曲角u，在渐近线即x或y轴上需要有的x或y的值1。显见这里的底边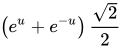是 ，垂线是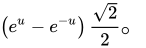

通过旋转和缩小线性变换，得到单位双曲线下的情况，有：

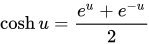
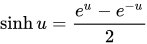
单位双曲线中双曲线扇形的面积是对应直角双曲线{\displaystyle xy=1}下双曲角的 1/2。

虚数圆角定义双曲角经常定义得如同虚数圆角。实际上，如果x是实数而i= −1，则

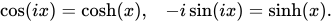所以双曲函数cosh和sinh可以通过圆函数来定义。这些恒等式不是从圆或旋转得来的，它们应当以无穷级数的方式来理解。特别是，可以将指数函数表达为由偶次项和奇次项组成，前者形成cosh函数，后者形成了sinh函数。cos函数的无穷级数可从cosh得出，通过把它变为交错级数，而sin函数可来自将sinh变为交错级数。上面的恒等式使用虚数i，从三角函数的级数的项中去掉交错因子(−1)，来恢复为指数函数的那两部分级数。

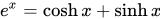
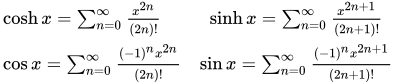
双曲函数可以通过虚数圆角定义为：

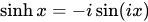
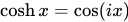
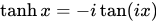
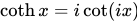
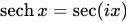
这些复数形式的定义得出自欧拉公式。

本词条内容贡献者为:

徐恒山 - 博士 - 西北农林科技大学